머신러닝 & 딥러닝/딥러닝 - Image classification
- 15. Batch size & Batch Norm 2018.08.19
- 14. Regularization 2018.08.19
- 13. Object Detection - two stage method(R-CNN, fast R-CNN, faster R-CNN) 2018.08.04 5
- 12. Data Preprocessing & Augmentation 2018.08.02
- 11. Optimization - local optima / plateau / zigzag현상의 등장 2018.08.02 1
- 10. transfer learning 2018.07.31
- 9. weight initialization - fan in 과 fan out / Xavior(Normalized) initialization의 등장 2018.07.30 2
- 8. activation function - saturation현상 / zigzag현상 / ReLU의 등장 2018.07.27 2
- 7. Pracical Usage of Convolution Layer - 3,3filter / zero padding/ strides / trade off / 1x1 C. Layer 2018.07.26 2
- 6. history of Deep Learning 2018.07.26
- 5. Convolutional Neural Network (이미지용 M.L.N.N.) - Convolution Filter / Max Pooling / keras 의 등장 2018.07.24 7
- 4. Multi-Layer Neural Network for XOR problem - Back propagation의 등장 / MNIST 성능올리기 2018.07.21
- 3. Single-Layer Neural Network For Multi-class classification문제 - 원핫인코딩 / argmax / MNIST의 등장 2018.07.17
- 2. Single-Layer Neural Network For Binary classification문제 - sigmoid의 등장 & squarshing 2018.07.17 2
- 1. Single-Layer Neural Network For Regression문제 2018.07.13
15. Batch size & Batch Norm
Batch size
batch size란 sample데이터 중 한번에 네트워크에 넘겨주는 데이터의 수를 말한다.
batch는 mini batch라고도 불린다.
이 때 조심해야할 것은, batch_size와 epoch은 다른 개념이라는 것이다.
예를 들어, 1000개의 데이터를 batch_size = 10개로 넘겨준다고 가정하자.
그러면 총 10개씩 batch로서 그룹을 이루어서 들어가게 되며, 총 100개의 step을 통해 1epoch을 도는 것이다.
즉, 1epoch(학습1번) = 10(batch_size) * 100(step or iteration)
하지만, batch_size가 커지면 한번에 많은 량을 학습하기 때문에, train과정이 빨라질 것이다.
그러나 trade off로서, 컴퓨터의 메모리 문제때문에 우리는 한번에 모두다 학습하는 것이 아니라 나눠서 하는 것이다.
즉, batch_size를 100으로 준 상태에서, 컴퓨터가 학습을 제대로 하지 못한다면, batch_size를 낮춰주면 된다.
실습
keras에서 batch_size의 선택은 fit()함수 호출 시 할 수 있다.
Batch Norm
data를 Neural Network에 train시키기전에, preprocessing을 통해 Normalize 또는 Standardize를 했다.
Regression문제에서는 사이킷런의 MinMaxScaler를 이용하여, 각 feature의 데이터를 0~1사이로 squarsh한 것이 예이다.
머신러닝이나 딥러닝은, 큰 수들을 좋아하지 않기 때문에 = 각 feature의 간격이 동일해야 편견없이 처리할 수 있다
(예를 들어, a feature는 0~13값을 가지고 b feature는 0~4값을 가지는데, 13을 4보다 더 큰 요소로 인식해버리 떄문)
Normalize나 Standardize는 모두, 모든데이터를 같은 scale로 만들어주는 것이 목적이다.
(Regularization은 weight를 줄이도록 loss를 변형(L2 Reg)하여, 모델의 복잡도를 낮추어 overfitting을 방지한다)
- Normalization : 구체적으로 10~1000 범위를 가진 feature를 --> 0~1값을 가지도록 Scaling한다.
- standardization : 각 데이터에 평균을 빼고 -> 표준편차를 나누어서 -> 평균0 표준편차1인 데이터로 변형한다.
- standardization 역시 Normalization으로 불리기도 한다.
이러한 작업을 하는 이유는 위에도 설명했지만, 아래 예를 다시보자.
miles Driven feature 와 age feature가 있다.
2 feature는 같은 Scale을 가지고 있지 않은 non-Normalized상태이다.
이러한 data는 Neural Network에서 불안정성을 야기한다.
즉, 너무 큰 범위의 feature값이 들어가게 되면, gradient를 태워 weigt를 업데이트할 때, 큰 문제가 발생하게 된다.
train하기도 힘들어지고, train속도도 느려진다.
하지만 Normalization을 통해 Scale을 0~1로 통일 시키면,
속도도 향상되면서, gradient를 태울 떄 문제가 발생하지 않게된다.
하지만 normalized된 데이터( scale통일 )도 문제가 발생시킨다는 것이 발견되었다.
train시 SGD로 그라디언트를 태워 w를 업데이트 하는 와중에
weight하나가 극단적으로 크게 업데이트되었다고 가정하자.
첫번째 hidden Layer에 도달하는 weight는 (8, 6)개의 matrix이다.
여기서 (4, 4)에 해당하는weight가 극단적으로 크게 업데이트 되었다.
이 weight에 상응하는 neuron (1hidden-4node)역시 커질 것이다.
그리고 다음 N.N.를 통과하면서 이러한 imbalance들이 문제를 야기할 것이다.
이 때 등장한 개념이 Batch Normalization이다.
비록 input data는 Normalization(0~1scaling)되었다 하더라도, weight가 커져버려 output도 커지는 상황이 발생한다.
정규화(loss를 변형하여, weight줄임->복잡도내려가고 variance줄임->overfitting방지)처럼,
Batch norm 역시 전체 모델 중 특정Layer를 선택하여 적용할 수 있다.
구체적으로는
이전Layer의 weight가 커져, 매우커저버린 output인 a(z(x))에다가
- activation funcion값을 Starndardization(평균0 표준편차1)을 만들어서,
- 임의의 상수를 곱함(trainable)
- 임의의 상수를 더함(trainable)
--> 다음Layer의 input이 되게 만드는 것이다.
이러한 과정을 거쳐 최적화 된 g와 b상수도 결정되게 된다.
Batch Norm은 gradient의 process에 포함되기 때문에, 특정weight가 극단적으로 커지거나 작아지는 것을 막아주게 된다.
결과적으로, input data는 Normalization을 통해 같은 Scale을 가질 수 있게 하여 --> 속도향상 + gradient problem을 막고
각 Layer의 output(a(z(x))에는 Batch Norm을 통해 같은 Scale을 가질 수 있게항 --> weight의 imbalance를 막는다.
- 이러한 과정은 모델에 input되는 Batch단위로 이루어지기 때문에, Batch norm이라 한다.
실습
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
| 14. Regularization (0) | 2018.08.19 |
|---|---|
| 13. Object Detection - two stage method(R-CNN, fast R-CNN, faster R-CNN) (5) | 2018.08.04 |
| 12. Data Preprocessing & Augmentation (0) | 2018.08.02 |
| 11. Optimization - local optima / plateau / zigzag현상의 등장 (1) | 2018.08.02 |
| 10. transfer learning (0) | 2018.07.31 |
14. Regularization
Regularization은 오버피팅(feature가 너무 많거나 지엽적인 데이터를 학습하여, 새로운 데이터에 대해서는 예측을 잘 못하는 것)모델의 해결방안 중 하나라고 언급된다.
정확하게는 복잡성을 줄여서 --> 오버피팅을 줄이거나 분산을 줄이는 것이다.
그 결과 training data에 대한 학습정도 <----> unseen data에 대한 일반화 정도를 trade off하는 것이다.
첫번째 간단한 방법으로는, 머신러닝 기초에서 설명한 것처럼, loss함수에 람다*(w1+w2+...+wn)을 붙히는 것이다.
이것은 상대적으로 큰 weight들에 작은 상수를 곱하여, weight를 줄이는 것이다.
더 일반적 많이 쓰는 Regularization은 L2 Norm을 가지고 정규화 하는 것이다.
즉 상수 람다/2m * ( 각 weight들의 제곱의 함)을 더하는 것이다.
그리고 이것의 의미는, 양수로서, 벡터공간 속에서 피타고라스와 같은 거리를 구하는 공식으로 생각하면 된다.
그리고 여기서의 m은 input되는 feature의 수이며,
람다는 regularization hyperparameter로서, 우리가 정하고 테스트해서 바꾸는 수이다.
요약하자면, 정규화란?
우리가 가진 weight들은 큰값도 있고, 작은 값도 있을 것이다. 큰 weight를 가진 feature는 모델에 크게 반영될 것이다.
하지만 L2를 이용한 정규화를 사용하여, loss함수에 제약을 걸면 상대적으로 큰 weight라도 다른 w와 비슷하게 w를 업데이트 시키게 된다.
그래서 상대적으로 큰 weight들도 작은 weight처럼 약하게 적용되는 것이다.
만약 람다(lr)를 높혔다고 가정해보자. 그러면 loss는 빠르게 w를 업데이트 시켜 0에 가까워질 것이다.
하지만 L2정규화를 통해 loss에 람다 * 양수가 곱해져있는 상황으로 loss혼자는 0으로 갈지라도 뒤에 값들이 더 커지게 된다.
그래서 전체loss는 2개의 합이므로 0에 수렴하진 않을 것이다.
그 결과 lr를 조절하는 것이 아니라,
결과적으로 loss전체를 최소로 만들려면 뒤에 더해진 weight들이 줄어드는 방식으로 w가 결정될 것이다.
w들이 줄어든다면
1)Regression문제에서는 해당 예측값h(x)의 전체적인 가파른 정도가 줄어든 것일 것이다.
2) 딥러닝에서는, 극단적으로 weight가 0으로 결정된다면, 해당 Layer는 사라질 것이다.
이러한 방식으로 복잡도를 줄여서, 마치 Dropout처럼 복잡도를 줄여나간다.
weight가 줄어들면, variance(분산)도 줄어든다고 한다. 그 결과 overfitting도 해결된다고 한다.
my)
Regularization은 loss 에 L2를 더해서, loss를 줄이려면 weight들을 줄여야한다.
낮아진 weight로 인해 모델의 복잡도도 줄어들면서, Overfitting이 해결된다.
실습
케라스에서는 모델전체의 loss에 l2정규화를 하는 것이 아니라, 각 Layer별로 정규화를 적용하여 overfitting을 방지하도록 해준다.
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
| 15. Batch size & Batch Norm (0) | 2018.08.19 |
|---|---|
| 13. Object Detection - two stage method(R-CNN, fast R-CNN, faster R-CNN) (5) | 2018.08.04 |
| 12. Data Preprocessing & Augmentation (0) | 2018.08.02 |
| 11. Optimization - local optima / plateau / zigzag현상의 등장 (1) | 2018.08.02 |
| 10. transfer learning (0) | 2018.07.31 |
13. Object Detection - two stage method(R-CNN, fast R-CNN, faster R-CNN)
지금까지 기초적인 부분과 튜닝에 대한 여러가지 기초지식을 배워왔다. 그리고 주로 이미지분류에 대한 공부를 많이해왔다.
이번에는 이미지 분류이외에도, 이미지에서 어떤 위치를 찾는 것에 대한 내용을 학습해보자.
크게, Localization, Detection, Segmentation이 있다.
3가지의 공통점은 모두 어떤 object에 대한 위치를 찾는 것이다.
차이점에 대해 살펴보자.
Localization : 고양이가 1마리 있다고 가정한다. 찾아서 박스를 친다.
Object Detection : 고양이나 강아지가 여러마리 있다고 가정한다. 찾아내서 박스를 친다.
Segmentation : 딕텍션과 비슷한데, 더 자세하게 픽셀단위로 보여준다.
이 3가지를 수행하려면, classification과 전혀다른 데이터셋이 필요하다.
지금까지 했던 classification의 dataset은 feature여러개 + label만 필요했다.
(feature1, feature2, ... , label)
하지만 Localization 의 dataset은 label + box의 x,y좌표, 가로,세로까지 필요하다
( C(label), x, y, w, h )
Detection의 경우, 박스가 여러개이므로, 저러한 dataset이 여러개 있을 것이다.
Segmentation의 경우, 박스의 x,y,w,h대신 , 14*14px이 있고, 거기에 0이면 고양이 없다 / 1이면 고양이 있다.의 형태가 될 것이다.
여기까지 이미지 위치찾는 것에 대해서,
1) 각 분야별로, 그에 맞는 가정이 있다.
2) 각 분야별로, 그에 맞는 dataset이 있다.
는 가정하에 진행된다. 이러한 dataset을 보유하기는 너무 힘들다. 공개되어있는 인터넷의 데이터셋을 사용하는 것에 크게 의존하고 있다.
여기서 Detection을 주로 다룰 것이다. Localization의 알고리즘은 거의다 Detection알고리즘으로 다 대체가 되었다고 한다. Segmentation은 아직 발전과제가 많이 남아있기 때문이다.
Localization 알고리즘
먼저, Localization이 어떻게 구성되었는지 알아보자.
앞서, Convolutional Layer의 Filter들은 각 이미지를 sliding window방식으로 좌상단에서부터 우하단까지 연산한다고 하였다.
Localization에서는 딥모델 전체가 Conv.Layer의 Filter들처럼, Sliding window방식으로 돌아다니면서, 강아지가 있는지 없는지 predict한다.
즉, 좌상단->우하단으로 딥러닝 알고리즘 통채로 1pixel씩 움직이면서 강아지가 있는지 없는지 predict하는 것이다.
움직이면서, '없다~ 없다~ 없다~' 하다가 강아지의 형체를 발견하면 predict의 확률을 높게준다.
마찬가지로, 아래칸에서 없다 없다 없다 하다가 있는 곳에서 predict의 확률을 높게 준다.
결과적으로, 곰이 있는 위치에는 확률를 높혀 노란색으로 / 중간정도는 보라색으로/ 없는 위치는 검은색으로
아래와 같이 표시된다.
이러한 Localization알고리즘(Overfeat 알고리즘)은 결과적으로는, 현재 쓰지 않지만 이러한 방식으로 작동하여 배울 점이 있다.
이 Overfeat알고리즘이 바로 이전시간에 다룬 (1,1) Convolution Layer로 발전했다는 것이다.
Fully-connected N.N. 대신 --> (1,1) Conv. Filter를 사용했을 때,
이미지를 더 큰 것을 집어넣을 수 있고, 잘 돌아간다.(FC layer는 input 이미지가 딱 정해진 것만 사용할 수 있었다.)
결과적으로 (1,1)이 나와야할 output이 ---> (2,2)로 나와서, 이것을 평균내는 것이 더 성능이 좋았다.
2015년까지는 이 Localization을 많이 사용하려 했었다. 왜냐하면 ResNet의 등장으로 인간의 분류능력을 뛰어넘으면서부터 ImageNet챌린지에서 2016년부터 classification경진대회를 없앴고 Classification+Localization대회를 만들었기 때문이다.
하지만, 2016~2017년 Localizaton경진대회에서 Detection알고리즘들이 우승을 해버렸기 때문에 지금은 Detection알고리즘이 메인이 되게 된 것이다.
Detection알고리즘
Localization과 달리, Detection은 기본적으로 한 이미지안에, 여러개의 Object가 있을 수 있고, Box도 여러개 칠 수 있다.
Detection알고리즘은 크게 2가지 방식이 있다.
- One-Stage Method : 속도가 빠름, ex> YOLO, SSD
- Two-stage Method : 정확도가 좋음, ex> R-CNN, Fast R-CNN, Faster R-CNN
먼저 나온 것은 Two stage Method이고, 최근에 나온 것이 One stage Method이다. One Stage 방식이 더 깔끔하고 구현도 쉽다.
실무에서도 One-Stage를 속도때문에 훨씬 더 많이 쓴다고 한다.
특히, 자율주행자동차에서는 realtime으로 예측해야하므로 실행속도가 중요하다. 그래서 One stage를 많이 쓰고, 발전 중이다.
Detection - Two Stage Method - R-CNN
Two stage method는 지금껏 학습한 것들이 순서대로 연결되어있으므로, 헤깔릴 수 있다. 그래서 순서를 인지하면서 학습해야한다.
먼저, 13년도에 출현한 R-CNN이다.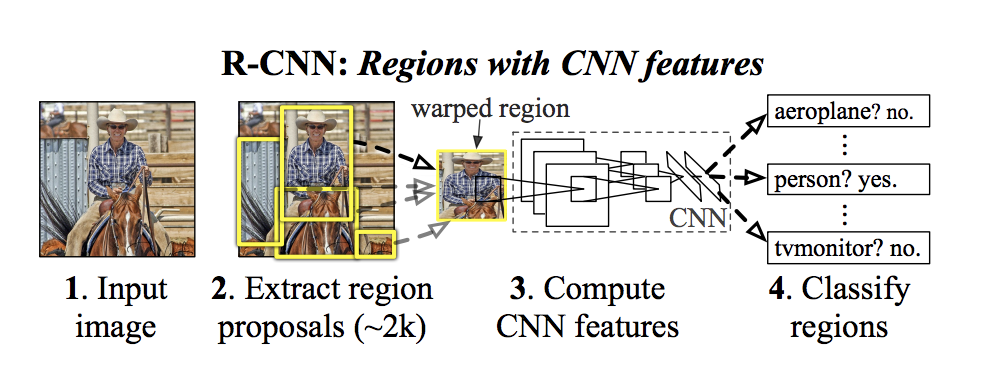
이 R-CNN이 two stage method인 이유는 기존알고리즘으로 먼저 찾고+ 딥러닝으로 다시 찾는 것, 2stage로 나눠져 있기 때문이다.
- 먼저, image classification 모델이 있다는 전제하에 시작한다. 그것을 transfer learning할 것이다.
- 13년에 나온 2 stage method의 시초라 할 수 있는 R-CNN은, 12년도에 사용되었던 AlexNet을 이미지classification 모델로 사용했을 것이다. - 가져온 classification 모델을 2개로 복사한다.
1) classification 모델 : 이미지에 고양이/강아지가 있냐 없냐를 판단하는 모델 -> classification을 맞춰야한다.
- 기존 classification모델은 1000개의 카테고리를 맞추는 imageNet챌린지용이었다.
- 너무 많으므로 기존 모델의 output Layer만 바꿔서 1000개
-> output(카테고리) 20개+(아무것도 detection못한 경우인 background)1 = 21개로 바꾼다.
2) Regression 모델 : Box를 쳐주는 모델 -> x,y,w,h를 맞춰야한다.
3) 2 모델을 따로 predict한다.
- 하지만 이 것만으로는 성능이 잘 안나와서 기존의 Detection알고리즘을 사용에 box후보군을 잘라서 넣어줄 것이다. - 기존의 Obejct detection 알고리즘 중 가장 성능좋은 Selective Search 알고리즘(region proposal)을 2개의 모델 앞에 적용한다.
- Localization처럼 sliding window방식은 아니지만, 전체 이미지 중 box쳐질만한 이미지의 일부분을 잘라주는 기존 Detection알고리즘이다.
- Selective search는 하나의 이미지에서 2000개의 box후보군을 잘라준다. - Selective Search(region proposal)로 쪼개진 이미지의 일부분을 CNN인 Classification모델 / Regression모델에 각각 넣어준다.
(참고로 SVM은, 서포트 백터 머신으로, loss용으로 쓰는 알고리즘 중에 cross-entropy / SVM이 있는데 SVM은 안쓴다)
결과적으로, VOC 2010 test 데이터셋(20개 카테고리)이 사용된 이미지넷챌린지 13년도 경진대회에서
기존 알고리즘들 + Localization알고리즘인 OverFeat를 사용하는 것보다
Detection알고리즘인 R-CNN을 사용하는 것이 성능이 월등히 좋았다.
참고로 mAP(mean Average Precision)는 예측한 Box와 정답Box의 일치정도라고 보면 된다.
참고)http://better-today.tistory.com/3?category=699736
R-CNN의 단점은 복잡+느린 것이다. 기본적으로 3개의 모델이 필요했다
- pre-trained된 classification모델
- 그것의 output개수를 고친 classification모델
- 그것으로 BoundBox의 x,y,w,h를 맞추는 Regression모델
- 이미지를 input할 때, Selective search로 후보Box들을 잘라내기 위해 2000번 자를 때, 속도가 너무 오래 걸린다. 그만큼 용량도 많이 필요한다. (이미지넷챌린지 이미지는 압축해도 60GB -> 한 이미지당 2000번 쪼개서 만드니 60 * 2000 GB..)
사실 Selective Search로 자른 2000장의 새로운 후보이미지들은 너무 용량이 크므로, 하드에 저장했다가 다시 꺼내서 쓴다고 한다. 용량 뿐만 아니라 속도도 어마어마하게 느려져서 개선의 여지가 필요했다.
즉, 결과적으로 모델을 줄이고(3->1) + 용량을 줄여 속도를 빠르게(Selective search의 순서바꿈) 하는 새로운 Detection알고리즘이 필요했다.
Detection - Two stage method - fast R-CNN
R-CNN과의 차이점은
R-CNN : 이미지를 먼저 Selective search로 2000개로 쪼갠것을 --> CNN에 넣느냐
Fast R-CNN : 이미지 1개만 CNN에 넣고 --> 나온 결과물을 Selective search로 2000번 쪼개느냐의 순서차이이다.
여기서 , CNN에서 나온 결과물(output feature)은 , RGB픽셀로 구성된 이미지가 아니라서 바로 Selective search에 들어가 쪼개질 수 없다.
그 output은 새롭게 뽑혀진 크고 작은 output feature일 뿐이다.
그래서 input image를
- CNN에 집어 넣기전에 이미지에 selective search(region proposal)을 먼저 돌려, 이미지를 어떻게 자를지에 대한 x,y,w.h 좌표만 구해놓는다. 그 좌표를 가지고 있는다.
- 이제 input image를 CNN에 넣으면 output feature(feature map)가 나온다.
- output feature는 이미지가 아니라서 selective search에 못넣었었다. 그러나
CNN을 통해 나온 output feature가, intput image에 비해 얼마나 작아졌는지 계산할 수 있다.
예를 들어)
(3,3) Convolutional Layer에 zeropadding을 넣었다면, input과 output 사이즈가 똑같았다.
여기서 maxpooling이 들어가면 가로세로 사이즈가 절반으로 줄었다.
이런식으로 CNN의 구조를 고려하여, input image의 사이즈가 얼마나 줄었는지 알 수 있다.
즉, output feature(feature map)의 사이즈를 유추할 수 있다는 것이다. - 그 유추한 계산을 바탕으로 + 1번에서 구해놓은 잘라야할 x,y,w,h좌표를 이용해 output feature를 2000번 자르면 되는 것이다.
이제 R-CNN에서 3개나 되었던 모델을 어떻게 줄여보자.
R-CNN에서는 Transfer Learning(CNN)모델을 --> Reg모델 / Classification모델 2개로 나누어서 따로 튜닝했었다.
Fast R-CNN에서는 Transfer Learning(CNN)모델을
--> 다시 1개의 모델로 만든 다음, output Layer만 2개로 나누어서, 따로 loss function구하고 따로 backpropagation하여 구한다.
--> 1개의 모델을 output만 2개로 나눈 효과는, classification와 regression의 backpropagation구할 때, 서로 긍정적인 효과를 미쳐 성능이 더 좋아진다 것이다.
그림에서 보면, Fully-Connected가 있다. 아직 13년도여서 (1,1) Convolution Layer에 대한 지식이 없었기 때문이다.
Fully-Connected의 단점은 input 되는 image의 사이즈가 서로 똑같아야한다는 것이다.
바로 직선에서 Selective search로 제각각 2000조각 난 output feature의 사이즈를 resizing해야만 할 것이다.
하지만 Output feature(feature map)은 이미지가 아니라서 resizing을 할 수 없다.
일반적인 R-CNN은 처음 Selecitve search시, 이미지를 크롭해준 것이기 때문에 resizing이 바로 가능했다.
Fast R-CNN은 resize해줘야할 것이 이미지가 아니라, output feature인 문제가 발생하는데,,,
이러한 문제를 어떻게 해결 했을까?
바로 Roi pooling이라는 것을 개발해서 해결했다. Max pooling으로 사이즈를 절반으로 줄이는 것과 비슷한 개념이다.
Selective Search(region proposla)에 의해 제각각으로 잘린 output feature(feature map)을 같은 사이즈로 변환하여
Fully-connected에 넣어주는 방식이다.
좀 더 구체적으로 예를 들면 (2,2) Maxpooling을 하면 사이즈가 절반으로 줄어들 것이다. 만약, (3,3) Maxpooling하면 그냥 퉁치고 넘어간다고 한다. 이것과 비슷한 것이 RoI pooling이다.
결과적으로 R-CNN보다, Fast R-CNN이 얼마나 빨라지는지 보자.
Train속도는 84시간 -> 8시간으로 줄었고, test속도는 49초 -> 2초로 준다.
(빨간색 그래프는 속도가 느린 Selective search( region proposal)을 뺐을 때 결과)
그러나, 요즘은 테스트시 2초도 느린편이다.. 예를 들어, 자율주행자동차에서 realtime으로 안되면,, 사고가 발생할 수 도 있을 것이다.
그래서 fast R-CNN의 단점인, 가장 성능이 느린 기존 알고리즘인 Selective search(Region proposal)하는 부분도 딥러닝으로 만들 수 있다.
Detection - Two stage method - faster R-CNN
fast R-CNN 중 전통적인 알고리즘인 Selective Search(Region proposal)부분을 딥러닝으로 바꾼 것을 RPN(Region Proposal Network)라 한다.
즉, 이 CNN기반의 미니 CNN인 Region Proposal Network가 이미지-> CNN 을 거쳐 나온 -> output feature(feature map)를 잘라준다.
RPN안에는 Convolution Layer에 심지어 fully-connected Layer도 존재한다.
RPN의 Convolution N.N.이 output feature를 sliding window방식으로 돌면서 연산후 classification 과 Regression연산까지 한다.
forward / backward propagation -> weight 업데이트 과정을 거치면 ---> Selective search를 대체하여 이미지를 2000box 조각낸다.
즉, CNN기반의 RPN이 sliding window방식으로 box를 찾는 역활한다.
이 때, box를 찾는 과정에서, 어떤 object는 가로가 길고, 어떤 object는 세로가 길어서, sliding window가 꼭 정사각형이 아니라 직사각형 형태로 도는 것이 유리할 수 있다. 이러한 여러형태의 sliding window를 anchor box라 한다.
그래서 RPN에서는 output feature인 feature map을 도는 여러개의 anchor box를 운영하고, 공식문서에서는 아래 형태의 4개의 anchor box를 운영한다.
즉, CNN의 필터 대신, RPN는 4개의 anchor box를 사용하여, 4개 따로 forward/backward하면서 training하여, 2000조각 낼 부분을 predict한다.
참고로 4개의 anchor box는, 개발자마다 설정(configuration이 가능하다)
요약 )
- image를 CNN에 집어넣는다.
- CNN에서 나온 output feature( feature map )을 Selective Search를 대체하는
Region Proposal Network에 집어넣어 classification 과 box얼마나 쳐야하는지를 따로 return받는다. - RoI pooling을 이용하여 box크기를 fully-connected에 넣을 수 있게 resizing해준다.
- fast R-CNN과 동일하게 해준다.
1개의 모델에 꼬다리만 classifcation / regression을 따로 만들어 loss2개, weight업데이트도 2개 따로하여
classification / regression(box위치)를 predict한다.
결과적으로 test시
R-CNN : 49초 ----------->Region Proposal(Selective Search)의 순서를 바꾸고, 모델 2개를 1개의 모델로 통합(꼬다리만 2개로)
Fast R-CNN : 2.3초 ---->Region Proposal(Selective Search)를 Region Proposal Network(CNN)으로 대체-->
Faster R-CNN : 0.2초
One-Stage-Method는 속도...
정확도를 위해서라면 우리는 Two-stage-Method인 Faster R-CNN을 쓰면 된다.
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
| 15. Batch size & Batch Norm (0) | 2018.08.19 |
|---|---|
| 14. Regularization (0) | 2018.08.19 |
| 12. Data Preprocessing & Augmentation (0) | 2018.08.02 |
| 11. Optimization - local optima / plateau / zigzag현상의 등장 (1) | 2018.08.02 |
| 10. transfer learning (0) | 2018.07.31 |
12. Data Preprocessing & Augmentation
Augmentation은 원래 데이터를 부풀려서 성능을 더 좋게 만든다는 뜻이다.
대표적인 케이스가 VGG모델에서 많이 사용하고 벤치마킹하였다.
VGG-D모델에서 256*256 데이터를 넣어주는 것보다 똑같은 사진을 256*256과 512*512 데이터를 따로 넣어주는 것이 미묘하지만 성능이 올라갔다.
에러가 3~5%까지 줄어든다고 한다.
기본적으로 Augmentation을 넣어주면, 기본적으로 성능이 좋아진다는 결론도 나왔다.
Augmentation
Augmentation을 하는 중요한 이유
1. Preprocessing과 augmentation을 하면, 거의 성능이 좋아진다.
2. 원본에 추가되는 개념이니 성능이 떨어지지 않는다.
3. 쉽고 패턴이 정해져있다.
단기간에 성능을 올리고 싶다면, 1) Transfer learning 2)Augmentation으로 해결하면 된다.
기본적인 예로,
1) 좌우반전
왼쪽만 바라보는 고양이를 70개를 넣어준다고 치자. 오른쪽을 보는 고양이는 못맞추게 된다.
왼쪽보는 고양이 70 + 오른쪽 고양이 70 총 140개를 넣어주면 어느쪽을 보더라도 다 맞추게 된다.
2)이미지를 잘라준다.
확률적으로 꼬리를 보고 고양으로 판단할 확률 50%, 귀를 보고 30%로 판단한다고 할 때,
고양이가 상자속에 들어가서 꼬리만 있는 사진을 사람은 꼬리만 보고도 고양이라고 판단할 수 있으나 딥러닝은 꼬리뿐만 아니라 상자도 인식하느라 고양이의 특징을 제대로 파악 못할 것이다.
사람을 인식방법을 모방하기 위해 사물+꼬리 있는 사진을 넣어주기 보다는, 꼬리만 잘라서 넣어준다면 더 성능이 좋아질 것이다.
각 부분만 보고도 고양이로 판단할 수 있도록 해준다.
3) 밝기 조절
만약 딥러닝 모델로 앱을 만들게 되면, 사진을 찍는사람마다 빛의 양이 다를 것이다. 다 인식할 수 있도록 어두운 것부터 밝은 것까지 밝기를 조절해서 다 넣어준다.
그 외에도 많은 응용방법이 있다.
AlexNet
이미지 챌린지에서 나왔던 AlexNet이라는 모델이 있다. AlexNet에서 처음으로 Augmentation을 heavy하게 썼다고 한다.
- 좌우반전
- 224*224px 를 ---> 256*256px로 resize한 다음 ---> 224*224px로 랜덤하게 2048번 잘라서 데이터를 2048배 늘림
- 테스트시에는 2048배 늘이면 너무 느리니까,
256*256px로 resize한 다음 ---> 좌상단/우상단/좌하단/우하단/가운데 5번만 잘라서 5배늘림 ---> 좌우반전까지 총 10배 늘림
---> 10개 따로 predict한다음, 평균을 낸다. - PCA를 통해 RGB채널을 조절하주었는데 요즘은 안쓰는 방식
VGGNet
사진데이터에서 가장 많이 사용하는 Preprocessing & Augmentation방식이 VGGNet이 했던 방식이다.
VGGNet은 굉장히 많은 방식으로 벤치마킹하고 실험했었는데 결과적으로
- RGB값을 각각 빼서, RGB값의 평균을 0으로 만든다 --> loss 수렴이 빨라진다.
weight초기화할 때도 E(X)와 E(Y) = 0에서 시작한 이유가, loss 수렴이 좋아져였다.
X와 Y는 모두 activation output이었다. hidden Layer 사이의 input과 output의 평균이 0인 것만 유지하도록 해주면 Layer를 더 쌓을 수 있는 개념이었다.
우리가 처음 이미지를 넣는 input은 세로,가로,RGB 값은 activation output이 아니므로
강제로 RGB값을 평균에서 빼주면, 사실상 input값의 평균이 0이 되어서 수렴이 빨라진다! - 같은 이미지를 256*256px, 384*384px, 512*512px 3가지 버전으로 만든 뒤,--> 224*224px로 랜덤 Crop한다.
256*256px에서 224*224px로 Crop하면 대부분의 이미지가 들어간다.
하지만 512*512px에서 224*224px은 이미지의 1/4정도밖에 안들어간다. 고양이로 치면 고양이 한마리 전체가 들어갈 일은 거의 없다.
즉, 고양이의 귀, 꼬리, 털 등등이 짤려서 들어간다. 사람처럼 일부만 보고도 고양이로 인식하도록 train되는 효과가 난다. - 테스트시에는 마찬가지로 하는 것이 가장 error가 낮았다.
결과적으로 이러한 방식으로 전처리를 하면 error가 10.4% -> 7.1%로 줄어들었다고 한다.
간단용어설명)
Multi-crop : Alexnet에서 했던, 좌상단~가운데 5개 크롭 + 좌우반전 2개 -> 10배 늘리는 방법
Dense : (1,1) conv Layer처럼 , Fully-connected Layer를 바꿔주면, test할 때 이미지를 더 크게 넣어 줄 수 있다. 크게 넣어주면 (1,1)으로 나오던 결과가 (2,2)로 나오는데, 그 결과값은 5군데 Crop하는 것과 동일하고, 그것을 평균내준다.
VGGnet에서는 Multi-Crop과 Dense를 따로 써주면, 성능이 좋아지지만 결과는 거의 비슷하고, 같이 써주면 더 성능이 좋아졌다.
굳이 따지면 실행속도가 빠른 Dense를 쓰는 것을 권장했지만, 결국엔 같이 쓰는 것을 택했다.
ResNet
VGGNet과 유사하므로 패스
그외 Preprocessing & Augmentation 방식
4) rotation : 0 ~360도 사이로 랜덤하게 회전시킨다. predict할 데이터가 회전된상태로 찍힐 가능성이 높다.
5) shifting : 랜덤하게 10px씩 상/하/좌/우 로 움직여준다. 그러면 외각쪽으로 고양이의 귀나 꼬리가 빠진 사진이 들어갈 것이다.
6) rescaling : 사진의 크기를 키우거나 줄이는 VGGNet에서 했던 방식. 보통 1.0 ~ 1.6배로 사진을 키운다.
7) flipping : 상하/좌우 반전, 좌우반전은 가장 많이 쓰는 방식이다.
8) shearing : 강제로 사진을 찌그러뜨린다. -20~ 20도 사이로 랜덤하게 해준다.
9) stretching : 강제로 랜덤하게 사진을 1.0 ~ 1.3배로 늘어뜨린다.
실무에서는 가장 성능을 끌어올리는 방식이 이 Preprocessing이다.
자신의 도메인 지식을 Preprocessing에 적용해야한다.
가주 자주 사용하는 방식은
- RGB 값의 평균을 빼는 것(99% 쓴다) -> 성능이 좋아지는게 아니라 train시 loss 수렴이 빨라진다.(Preprocessing)
- 좌우반전(Augmentation)
- 다양한 사이즈로 넣기(Augmentation)
요즘은 overfitting을 방지하기 위한 Random noise방식은 거의 쓰이지 않는다고 한다.
실습
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
| 14. Regularization (0) | 2018.08.19 |
|---|---|
| 13. Object Detection - two stage method(R-CNN, fast R-CNN, faster R-CNN) (5) | 2018.08.04 |
| 11. Optimization - local optima / plateau / zigzag현상의 등장 (1) | 2018.08.02 |
| 10. transfer learning (0) | 2018.07.31 |
| 9. weight initialization - fan in 과 fan out / Xavior(Normalized) initialization의 등장 (2) | 2018.07.30 |
11. Optimization - local optima / plateau / zigzag현상의 등장
지난시간까지는 weight 초기화하는 방법에 대해 배웠다. activation func에 따라 다른 weight초기화 방법을 썼었다.
그렇게 하면 Layer를 더 쌓더라도 activation value(output)의 평균과 표준편차가 일정하게 유지되어 성능이 유지되었다.
예를 들어,
sigmoid, tanh에서는 Xavior initialization(Normalized initialization) - keras에서는 glorot_intialization
relu에서는 He initialization
오늘은 3가지 딥러닝 튜닝의 마지막 시간이다.
activation func -> weight initialization -> optimization
Optimization
코드상 Multi-Layer Neutral net / feed-forward Neural net은 아래와 같았다.
Optimizer는 실제로 Gradient descent로 w를 업데이트 하는 알고리즘이라고 보면 된다. 그리고 이 optimizer는 튜닝할 여지가 많이 남아있다.
최근에 Optimizer가 논란거리가 있다고 한다. 이론적으로 검증이 안되었음에도 벤치마킹에 의해 퉁치고 넘어가는 경우가 많았다.
벤치마킹 결과가 잘나오면 그게 대세가 되는 것이다. 그런데 알고봤더니 그게 그렇지 않은 경우가 있다.
2017년 후반과 2018년에 Optimizer를 이해 및 쓰는 알고리즘 트렌트가 바뀌었다고 볼 수 있다.
간단한 Overview를 해보자. 앞에서 우리는 Gradient Descent 알고리즘를 배웠다.
Cost(Loss)의 w편미분을 통해 w의 변화량을 구해서 가져와, Gradient Descent를 태우면 랜덤으로 초기화된 w라 하더라도 어느순간 좋은w를 찾아가는 train이 이루어진다.
그라디언트 디센트를 이해하기 위해 2차원(x축 w는 1개 뿐 - y축 cost(loss) func)의 그래프를 학습했었다.
초기화된 랜덤한 w점에서 Graident Descent가 업데이트 시키기를 점점 접선기울기가 0인 지점(cost or loss 최소값)을 찾아갔었다.
그 이동하는 간격이 동일하게 톡톡~ 이동할 것 같지만, 그렇지 않고,
w를 업데이트를 하는 순간, 기울기가 가파른 순간에는 크게 내려간 다음 ,기울기가 작아지면 조금씩 업데이트 된다.
하지만 Gradient를 태워 w를 업데이트 시킬 때 중요한 문제 중 하나가 아래와 같은 Cost(loss)를 가질 때다.
평평하게, 뭉뚝하게 생긴 부분에서 업데이트 속도가 매우 느려지는 문제이다.
ReLU를 activation function으로 쓰면, cost 함수가 아래와 같이 뭉뚝한 부분이 없어져서 업데이트 속도가 빨라진다.
그러나 ReLU사용이 불가능한 경우도 있고, 미분가능함수를 사용하다보면 뭉뚝한 부분 많은 경우도 많기 때문이다.
실제로 train 시키다 보면, 100번 train시킬 때,
한 3번 정도는 loss가 처음에는 툭! 떨어지다가, 97번은 계속 제자리에 멤도는 수준으로 느리게 w가 업데이트 된다.
이러한 문제를 해결하기 위해, Optimization(그라디언트 태우는 알고리즘)을 무엇으로 선택할지가 중요한 문제이다.
Local Optima(minimum)과 Global Optima(minimum)
어떤 Loss function이 있을 때, 그것을 시각화해서 이해했다.
맨 처음 이해를 위해, Regression문제를 해결하는데 있어서, loss function을 MeanSquareError(2차 함수)를 학습했다.
하지만, 실제 우리가 loss function을 사용할 때는, 단순한 2차 함수만 나오는 것이 아니다.
아래와 같은 울퉁불퉁한 n차 함수가 나올 수 있다.
.초기화w에서 시작하여, graident descent를 타고 내려갔는데,,
아직 최종목표(loss 최소값 = Global Optima)에 도달하지 않았음에도 불구하고.
어느 지점에 들어가니까 평평하고, 더 진행하려다 보니까 loss가 늘어나므로, w를 멈추게 된다.
이러한 지점을 Local Optima(minimum)이라 하고, Optimization을 잘못한 경우 로컬옵티마에 빠지기 쉽다고 얘기한다.
하지만 요즘 trend에 의하면, 로컬옵티마는 중요한 문제가 아니라고 한다.
실제 딥러닝에서는 로컬옵티마에 빠질 확률이 거의 없기 때문이다.
위의 그래프는 w가 1개인 모델이지만 실제 딥러닝 모델에서는 w가 수도없이 많으며, 그 수많은 w가 모두 로컬옵티마에 빠져야 w업데이트가 정지되기 때문이다. 이론적으로는 그것이 불가능하기 때문에
로컬옵티마를 해결하기 위해서 Optimization을 할 이유는 없다고 보면 된다.
기존에는 로컬옵티마를 해결하기 위해 Optimization을 한다고 했었지만... 로컬옵티마는 고려할 필요는 없다고 하는 것이 추세다.
그렇다면 요즘에 Optimization을 쓰는 이유는 무엇일까?
Plateau
아래와 같이 w가 저 위치에 초기화 되었다고 가정해보자.
Gradient Descent를 타고 Global Optima를 향해서 나아가는데, 평지(Plateau)가 생겨 통통통 튀다가 더이상 loss가 업데이트 되지 않는 현상이 발생한다. 이러한 것을 Plateau현상이라 한다. 그리고 이 플래튜현상이 로컬옵티마에 비해 발생확률이 무지하게 높다.
예를들어, w가 2개(x축, y축)이고, loss를 점으로 찍는 scatter(3차원)를 그린다고 가정해보자.
이러한 평면에서, x축과 y축이 동시에 평평해질 확률은 꽤 높다고 한다. 실제 우리가 살고 있는 지구를 봐도 그렇다.
x축과 y축이 있다고 가정하면 평평한 땅이 얼마나 많은 가?
아무리 w가 늘어나더라도 Plateau는 항상 발생한다는 것을 알 수 있다.
우리는 이 Plateau현상을 극복하기 위해서 Gradient를 Optimization할 것이다.
Zigzag현상
이전에 지그재그 현상에 대해서 배웠다. dL/dw2 를 체인룰로 풀 때, 3개의 곱 중에 2개가 양수로 부호가 같이 나오는 sigmoid or ReLU를 사용하는 경우에는, w업데이트 행렬의 부호가 모두 동일하여, 원하는 방향으로(+ 과 - 조합)으로 못가서, 지그재그로 w목표점을 찾아가는 현상이었다.
Gradient Descent를 시각화하는 방법 중 하나로, w가 2개인 loss(cost)function의 3차원 그래프를
등고선을 활용하여 scatter형식으로 2차원으로 그려보자.
이번에는 조금 찌그러진 gradient( Skewed gradient)을 시각화해보자.
w1방향(x축)으로는 길고, w2방향(y축)으로는 짧은 구조이다.
- w1 폭 넓다 -> 업데이트는 많이 해줘야하지만, 3차원상으로 완만하여 조금밖에 못간다
- w2 폭 좁다 -> 업데이트를 조금만 해줘야하지만, 3차원상으로 가팔라서 많이씩 간다.
이러한 Skewed gradient에서는 ZigZag현상이 일어날 수 밖에 없다.
결과적으로 좋은 Optimization 알고리즘( gradient태울 때, w변화량 구하는 알고리즘)은
1) Plateau 현상을 해결해서 w를 업데이트 해준다.
2) weight space가 Skewed된 Gradient에서 이러하는 ZigZag현상을 해결해서 업데이트 해준다.
지금까지 쓴 Gradient Descent 알고리즘(SGD)은 Local Optima, Plateau, ZigZag현상을 해결하진 못한다.
그럼 어떤 Otimization 알고리즘을 사용해서 Gradient를 태워야할까?
Optimizer의 종류
Optimization 알고리즘(gradient 태우는 방식)의 개선된 방식은 크게 모멘텀 방식과 어댑티브 방식 2가지로 나뉜다.
우리가 여태 썼던 optimizer는 sgd(keras기준, stochastic gradient descent)이다.
- sgd : 언제나 느리다.
1. 모멘텀 방식의 optimizer : 속도를 최대한 빠르게!
- 초록색(momentum). 보라색(nag, Nesterov Accelerated Gradient = Nesterov Momentum) : 스타트부터 엄청빠르게 global optima에 들어간다. 휘기는 하나 엄청 빠르다.
- 단점 : 속도는 빠르지만, skewed된 weight space에서는 휜다.
2. 어댑티브 방식의 optimizer : 방향을 최대한 일직선으로!
- 파란색(adagrad) ,노란색(adadelta), 검은색(rmsprop) : 속도는 빠르지 않지만, skewed한 상황에서도 지그재그없이 일직선으로 들어가려 한다.
- 단점 : 속도는 느리다.
이 Optimization 의 2가지 방식에서는 작년(2017)과 올해(2018)과 트렌드가 달라졌다.
작년까지는 모멘텀 + 어댑티브 방식을 합친 Adam 알고리즘을 선호했는데
요즘엔, 어댑티브 방식이 크게 쓸모없다는 여론이 커졌다. 그래서 모멘텀 방식 위주로 가고 있다고 한다.
결과적으로, 우리는 Optimizer를 고를 때,
Momentum 방식인 adagrad or rmsprop을 고르면 된다.
Optimizer을( Gradient 태우는 알고리즘) 하나씩 살펴보자.
1. 가장 기본적인 SGD(Stochastic Gradient Descent)
cost function 편미분 -> 접선의 기울기를 가지고 w업데이트하는 방식의 gradinet
-> 단점 4가지(뭉뚝한부분에서 느림, 로컬 옵티마, 플래튜, 지그재그현상) 를 모두 가져서 w도달까지 오래걸린다.
2. Momentum -> 단점 4가지 중 3가지를 해결한다.
sgd가 cost func을 편미분(접선의 기울기)를 가지고 w를 업데이트 했다면,
momentum은 현재의 기울기 + 이전의 기울기를 포함하여 누적된 가속도로 w를 업데이트를 함. (관성의 개념)
간단히 말해, 현재 w를 업데이트할 때, 이전 w업데이트량만큼 계속 가속도를 붙혀, 업데이트 속도가 빨라진다.
그 결과,
- 뭉뚝한 부분에서, 현재의 속도가 느려서 업데이트 못했었는데, 이전 업데이트량이 포함되어있으니 그 구간에서도 스피드가 빨라짐
- 로컬 옵티마에서, 타고내려가다가 현재가 평평해서 업데이트 안해줄 상황에서도, 이전 업데이트량에 의해 통과해버린다.
글로벌 옵티마에서도 뛰어넘는 현상이 발생하여(위의 그림) loss와 accuracy를 보면 튀는 현상이 있는데, 결국엔 돌다가 들어온다.
- 플래튜에서, 현재 그라디언트(접선의 기울기)는 0이지만, 이전의 업데이트량이 포함되어, 계속 진행된다.
(지그재그현상은 해결안된다.)
코드상에서 원리를 살펴보자.
1) dw1( 이전 w업데이트량 )을 캐싱하여 가지고 있는 상태에서,
2) mu(뮤)라는 dw1 반영 비율(보통 0.9)을 생성하여 반영시켜주면 된다.
3) 현재 업데이트량에 더해서 업데이트 시켜준다.
그러면 w업데이트속도가 빨라져서 3가지 단점을 해결할 수 있다.
Momentum의 단점은 Global Optima에서도 이전 가속도가 더해지기 때문에, 추월하는 현상이 발생하는 것이다.
그래서 이전 가속도를 조금 더 줄여서 반영하고 싶은데, 그러한 Optimizer가 바로 Nesterov Momentum이다.
3. Nesterov Momentum
Momentum은 현재 그라디언트(접선의기울기, w업데이트량)과 이전 누적된 그라디언트를 각자 구해서 더한다고 했다.
Nesterov Momentum은
1) 먼저 Momentum을 먼저 진행한 상태에서,
2) 그 상태에서의 그라디언트를 계산하여 더하면,
추월하는 현상이 줄어든다.
코드상으로는 너무 복잡하므로 변형공식을 이용해서 코드를 작성한다.
모멘텀처럼, 현재 그라디언트 +이전 그라디언트를 모두 구한다음에, 이전 그라디언트의 누적치를 빼주는 방식으로 쓴다.
결과적으로 momentum보다 추월을 좀 더 하는 느낌이다.
하지만, 성능이 너무 크게 향상되지 않기 때문에
우리는 default Optimizer로 Momentum을 쓰면 된다.
4. AdaGrad ( 어댑티브 방식 ) : 속도를 높이는 것보다, 일직선으로 향하게 하는 방식 첫번째
요즘은 쓰지 않는 어댑티브 방식이다. 하지만 내부적으로 모멘트 방식과 섞으려는 연구가 진행중이다.
작년까지는 Adam이라는 알고리즘이 대세였지만, 어댑티브 방식이 안좋다는 증명때문에, 모멘트 방식을 주로 사용한다.
하지만 경험적으로 모멘텀 방식( 모멘텀, 네스테로브 모멘텀)보다 가끔, 어댑티브 방식인 RMSProp이 성능이 더 좋을 때도 있다. 하지만 이유가 증명되지 않았기 때문에, 아직까지는 모멘텀만 사용하기를 권하고 있다.
어댑티브 방식은 Skewed 상황에서 w1/w2의 필요한 업데이트량과 정반대로 업데이트되어 느린 zigzag 현상을
각 w의 업데이트량을 보정해서 해결하는 방식이 AdaGrad이다.
아래 그림처럼, SGD나 모멘텀방식은 속도만 빠를뿐, Skewed한 weight space에서 zigzag현상을 해결하진 않는다.
어댑티브 방식인 AdaGrad를 사용할 경우, w1, w2의 업데이트량을 보정하여 휘는 정도가 줄면서 일직선에 가깝게 w를 업데이트한다.
w1을 그냥 대입하는 것이 아니라, 제곱한 것을 캐슁해놓고 루트씌워서 w1업데이트량에 나눠서 보정하는 방식이다.
1) dw1의 현재 그라디언트(접선의기울기, w1 업데이트량)를 제곱하여, (-)음수도 양수가 되게 한다. 그 부분을 캐슁해놓는다.
2) 거기다 루트씌워서 크기만 원상복귀하여 마이너스만 제거한다.
3) 이제 w1업데이트부분에서 dw1이 아닌 dw1 / 루트( 캐싱한 부분 )을 나누어준다.
업데이트량이 크다면 크게 나누어지고, 작으면 작은값을 나누어주어서, Normalization효과가 일어나게 된다.
첫번째 업데이트시에는, 제곱한걸 더해서 캐슁해놓는 부분이 없기 때문에, 업데이트량 dw 부분은 1이 될 것이다.
하지만 그 다음부터는 이적 누적치가 반영되기 때문에,, 이전에 뛴만큼 누적치로 나누어줘서 보정된다.
결과적으로는 w1과 w2의 업데이트량이 비슷해지는 효과가 난다. -> 가능한 일직선으로 업데이트 된다.
cf) 0.000001 을 넣어주는 이유는, 나눗셈시 혹시나 0이 나올 때를 에러방지하기 위해, 아주작은 양수를 넣어두는 것
요약 ) 제곱하고 루트씌워서, 양수의 자기자신을 만든 다음에, 나누어주는 것! + 제곱부분해준 부분만 누적되어 캐싱
AdaGrad의 단점은?
실행하면 실행할수록 느려진다. 그 이유는 제곱부분(루트씌우기전) 캐싱부분에서는 끊임없이 누적되기 때문에..
나누어주는 수가 커지니까 w업데이트가 너무 느려진다. 결국엔 0이 될 것임.
5. RMS Prop(어댑티브 2번째 방식) : AdaGrad를 개선한 어댑티브 방식
AdaGrad가 제곱부분을 계속 캐슁할 때, 캐쉬값이 너무 커져서, 업데이트량에 나누어주는 값이 너무 커져 업데이트가 안되는 현상이 발생했다.
이 때, 이전에 제곱되어 누적된 캐슁되어있는 값과 새롭게 제곱되는 부분의 반영비율을 decay라는 상수로 반영비율을 조절한다.
마치, Momentum의 mu로 이전 업데이트량이 더해지는 부분의 반영비율을 조절하는 것과 마찬가지다.
만약, decay가 0.9라면, 이전의 누적된 그라디언트의 제곱은 90%반영해서 누적, 현재 그라디언트의 제곱은 10%반영 되는 것이다.
만약 속도가 느려졌다면, decay를 줄여 캐쉬값의 반영을 줄인다면, 나누는 부분이 작아져서, 업데이트 속도가 올라갈 것이다.
이렇게 개발된 RMSProp은 토론토 교수가 논문으로 작성하지 않아서, 인용이 안된다는 재밌는 소식이 있다.
작년까지 가장 좋은 Optimization 알고리즘은 Momentum + RMSProp을 섞어쓴 Adam이었는데, 지금은 모멘텀이 대세라고 한다.
그런데, 경험적으로, 모델을 train하다보면 RMSProp이 좋을 때도 있다.
결과적으로, Momentum을 쓰고 잘 안된다 싶으면, 한번씩 RMSProp으로 바꾸어 lr,deacy를 잘 조절하면 성능이 좋아진다. (증명되진 않음, 논문도 없음)
cf)
Optimization의 방식은 크게 2가지가 있다.
- Iterator방식(Gradient를 태워 backpropagation을 이용해서 for문을 돌면서 w업데이트) : 응용이 가능하고 범용적인 방법
- 수학적방식 : ...?
6. Adam : Momentum(모멘텀 방식) + RMSProp(어댑티브 방식)을 섞은 것
작년까지 대세였던 Optimization 알고리즘이 바로 이 Adam이다.
모멘텀방식 ( 아래 파란색 ) + 어댑티브 중 RMSProp 방식( 아래 빨간색 )을 합쳐놓았다.
이 때, mu와 decay 대신 beta1 과 beat2를 decay방식( decay, 1-decay)으로 사용된다.
보통 beta1은 mu처럼 0.9를 , beta2는 decay는 0.99를 사용한다.
1) 현재의 그라디언트를 구한다(dw1)
2) dw1m에다가 현재의 그라디언트를 더해서 계속 누적시키는데, beta1이라는 상수를 사용해서, 누적량과 현재량의 반영비율을 조절한다.
3) dw1v에다가 현재의 그라디언트틀 제곱해서 계속 누적시키는데, beta2라는 상수를 사용해서 ,누적량과 현재량의 반영비율을 조절한다.
4) 그리고 더해서 누적한것 에다가 루트 (제곱해서 누적)시킨 것을 나누어서 업데이트량으로 삼는다.
Adam에서 decay를 beta1을 0.9를 사용한다고 했다.
첫 epoch에서는 캐쉬값이 없기 때문에, 0.9* 0 + 0.1 * 현재 그라디언트 값이 캐슁될 것이다. 그러면 0.1만 반영되므로
초기 w업데이트 속도가 느릴 것이다. 이게 Adam의 단점이다.
결국에는 빨라지긴 하나, 초기에 느려지는 것이 싫을 때 쓰는 방식이 Adam의 Warm start버전이다.
7. Adam w
4, 5번째 줄에 dw1mb와 dw1vb가 새로 생겼다. 기존 Adam의 dw1m, dw1v를 epoch을 이용해서 보정해준다는 의미일 것이다.
첫 루트의 dw1mb를 보자. 코드상으로는 epoch은 0일 것이다.
1) 1 + epoch = 1
2) beta1 의 1제곱 -> beta1 그대로 0.9
3) 1 - beta1 = 0.1
4) dw1m에 0.1를 나눔 = 10을 곱한 것 --> 업데이트량도 10배 늘어난다.
5) epoch이 늘어남 -> beta1인 0.9(소수점)의 제곱 승수가 커짐 (전체값 줄어듬) -> 1 에서 더작은량이 빠짐 -> dw1m에 더 큰값이 나눠짐 -> dw1mb 작아짐 -> 업데이트량 작아짐
-> 초반에 느려진 것을 epoch을 이용해서 초반에 빠르게 하고, epoch이 커질 수록 dw1m에서 나누어지는 값이 1에 가까워서 Adam처럼 됨.

등고선이 굉장히 꼬여있는 Skewed된 상황에서
sgd : 안가는 수준
Momentum, Nesterov Momentum (모멘텀) : 가속도로 확치고올라가지만, 많이 휜다.
AdaGrad, RMSPROp (어댑티브) : 빠르진 않지만 zigzag없이 일정한 방향을 유지할려고함
Rmsprop > Adagrad (어댑티브가 먼저 들어감) -> Nesterov M -> Momentum -> SGD는 거의 안감
이것을 보면, 어댑티브가 좋은 것 같지만, 요즘은 성능이 안좋다는 이유로 모멘텀을 쓴다.
결과적으로 우리는 Optimization 알고리즘으로
Momentum을 쓰고, 안되면 RMSProp도 한번씩 써보자.

실습
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
| 13. Object Detection - two stage method(R-CNN, fast R-CNN, faster R-CNN) (5) | 2018.08.04 |
|---|---|
| 12. Data Preprocessing & Augmentation (0) | 2018.08.02 |
| 10. transfer learning (0) | 2018.07.31 |
| 9. weight initialization - fan in 과 fan out / Xavior(Normalized) initialization의 등장 (2) | 2018.07.30 |
| 8. activation function - saturation현상 / zigzag현상 / ReLU의 등장 (2) | 2018.07.27 |
10. transfer learning
딥러닝은 아주 강력한 모델이지만, 진입장벽이 높다. 3가지 이유를 생각해보자.
1) 충분한 양의 데이터
2) 고성능 하드웨어(GPU)
3) 딥러닝으로 구현한 알고리즘 및 튜닝 노하우
3가지 중에 Data를 구하는 것이 가장 큰 문제라 볼 수 있다.
이미지 데이터를 구하는데 어려움을 겪고, train시키는데 너무 많은 시간이 소요된다.
하지만, train시킨 결과물(weight)은 용량이 적다. 그리고 train시간보다 predict(예측)하는데는 시간이 별로 걸리지 않는다.
아무리 복잡한 모델이라도, train된 결과물(weight)를 가져와서 예측한다면, 고성능 하드웨어 없이도 가능하다는 말이 된다.
이미 누군가가 만든 알고리즘 모델을 가져와서 쓰는 것을 transfer learning이라고 한다.
Transfer learning
하지만, 아무리 큰 기관이라도 모든 데이터를 학습시켜놓진 않는다.
대안으로서, (ResNet은 마이크로소프트. GooGleNet은 Google이) 이미지넷을 가지고 학습시킨 완성된 딥러닝 모델을 가져오게 되면, 우리가 새로만드는 모델보다 성능이 훨씬 좋을 것이다.
이미지넷 데이터도 모든 데이터가 있는 것이 아니기 때문에, 우리가 우리 데이터에 맞추어 마지막단계에서 train만 시켜주면 된다.
예를 들어, 이미 학습이 끝난 VGGNet모델을 다운받고, 마지막 Fully-connected N.N.만 없앤 뒤, 자신이 보유한 데이터에 맞게 마지막 Outpt Layer를 완성한 뒤, 이 Layer에서만 train시키면 되는 것이다.
왜냐하면, 이미지넷 챌린터의 목적(label)은 1000가지 카테고리를 판단하는 것인데, 우리는 필요한 만큼의 label만 분류해주면 되기 때문이다.
이 때, 앞의 Layer의 output neuron에 대해서는 weight는 랜덤초기화가 들어가게 된다.
이미지넷 챌린지로 train된 Conv. Layer들은 feature만 뽑아놓은 상태이기 때문에, 우리는 Single-Layer N.N. 등으로 다시 train시킨다면, 그냥 우리가 모델을 만들어서 쓰는 것보다 언제나 결과가 좋다고 한다.
즉, 꼬다리만 떼고, 마지막 Layer만 train시키고, 앞의 weight들은 건들지 않으므로 train속도가 훨씬 빠르다.
그림상의 VGGNet모델 같은 base모델을 backbone모델이라고 한다. 백본을 활용해서 모델을 구성해야한다!
데이터가 너무 많을 때는, 약간 앞의 레이어도 같이 학습할 수 있다.
이러한 weight학습 세팅은 keras에서 모델구성시 수정할 수 있다.
transfer learning전까지는 하나의 딥러닝 경진대회마다 새로운 알고리즘이 나왔었다.
하지만 T.L. 이 등장하여. 마지막 Layer만 수정하여 자신이 분류하고 싶은 label만큼 output을 수정한 결과
모든 알고리즘을 다 이겼다는 후문이다..ㄷㄷㄷ
결론적으로 무슨 경진대회든, 데이터가 작을수록 가능한 transfer learning을 하면된다.
요약하자면)
오픈된 이미지넷 챌린지 train완료 모델을 다운받아서, output Layer만 수정하여 train시키면 되므로 하드웨어성능이 많이 크게 필요하지 않는다.
백본모델을 갈아끼우는 식으로 하면 모델 학습하기가 쉬워진다.
Transfer 모델도,, 이미지 챌린지 카테고리에 걸린 것들만 성능이 좋아진다.
만약 없는 데이터라면,, 분류가 안된다.
실습
VGGNet을 백본모델로 하여, keras를 이용해 빨간줄 친부분까지를 완성시켜보자.
keras로 VGG16을 백본으로 고양이/개 binary classification + 히스토리 + 평가까지
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
9. weight initialization - fan in 과 fan out / Xavior(Normalized) initialization의 등장
지금까지...
현재까지는 python으로 M.L.N.N.(feed-forward N.N. = fully-connected N.N.)모델을 구현할 때, 성능을 높이는 방법으로는
1) activation func-> ReLU를 쓰자.
2) weight 초기화
3) optimizer를 바꾸기
activation func으로는 ReLU를 쓰면 된다고, 했다. 그외 성능을 올리고 싶으면 다른 것을 쓰면 된다.
이번시간에는 weight initialization에 대해서 공부해보자.
Weight initialzation
weight 초기화는 14~15년도 사이에 발생한 최근 트렌드라고할 수 있다.
그전 까지는 weight초기화로 성능 개선할 수 있다는 인식이 약했다. 처음 초기화만 하면 gradient를 태워서 업데이트 하면 되기 때문이다.
하지만, 최근에 weight를 어떻게 초기화 하냐에 따라서 성능이 달라지는 것을 발견하고 관심을 가지기 시작했다.
weight는 Layer의 타입, neuron의 개수, activation func의 종류 등 여러 configuration에 대해 연관이 있다. 그러기 때문에 공통format을 만든 뒤, 이것을 수정하는 방식으로 사용하면 매우 효율적일 것이다.
예를 들어, activation func을 sigmoid를 썼을 때, tanh를 썼을 때, ReLU를 썻을 때 마다 공통format을 기준으로 미묘하게 수정할 것이다.
그 전에 M.L.N.N.(feed-forward N.N. = fully-connected N.N.)에서 weight 초기화에 따라 모델의 성능을 한번 살펴보자.
weight initialization에 따른 error(낮으면 수렴)를 각 Activation functon 별로 나타낸 것이다.
먼저,
- Sigmoid 사용시, Layer가 depth4 -> depth5로 1개의 Layer가 추가되는 순간 에러가 굉장이 높아지면서 수렴하지 않는다
- Sigmoid를 -> tanh로 바꾸니까 성능이 좋아진다.
- tanh N은 tanh를 weight initialization을 잘한 Normalized initialization이다.
같은 activation func이라도, weight초기화만 잘해줬더니, error가 더 낮은 값으로 수렴한다.
일반적으로는 Normalized initialization을 Xavior initialization으로한다.
결론적으로, 똑같은 딥러닝모델에서 weight를 잘 초기화하냐 하지않느냐에 따라서 성능이 바뀌는 것을 알 수 있다.
여태껏 해줬던 weight초기화 방식을 먼저 살펴보자.
-1.0 ~ +1.0에서 uniform분포(주사위 던지기)로 랜덤 초기화 했다.
하지만 이러한 방식은, simple한 data에서나 통하지, M.L.N.N.시 사용하면 수렴이 잘 안된다. lr를 조절하더라도 결국 error가 수렴하지 않는다. Layer를 1개만 썼을 때는, 수렴했지만, Layer를 늘려가면 갈수록 수렴하지 않는다.
이러한 방식을 Small Random Number 초기화 라고 하는 데, 모델이 수렴하지 않는 이유 중 weight 초기값을 잘못설정하는 것도 적지 않는 이유가 되는 것이다.
Small Random Number 초기화( -1 에서 +1 까지 uniform분포로 weight초기화) 방법이 왜 잘못되었는지 알아보자.
먼저 Hidden Layer가 2개이며, 각 neuron의 개수가 100개인 M.L.N.N. 모델에서,
Sigmoid를 activation func으로 사용하고 있다고 가정해보자.
첫 Hidden Layer의 neuron값들은 sigmoid를 거쳐서 나온 0~1의 범위를 가지는 100개의 neuron일 것이다.
두번째 weight를 -1 ~ 1 사이값으로 초기화 했다고 가정해보자.
input과 weight2의 dot product결과인 z의 범위는, input 0 ~ 1사이에서 모두 1이 나오고 weight는 모두 -1이 나오면
최소값은 -100 이다. 반대로 weight가 모두 1이 나오면 최대값은 100이다.
여기서 activation(a)값을 시각화 해서보면, 모두 saturation현상이 발생하게 되어, 결국에는 w업데이트가 멈출 것이다.
즉, weight를 - 1 ~ +1로 초기화 하게 되면 (잘못초기화),
activation func으로 넘어가는 input값이, saturation되는 값으로 넘어오게 된 순간 train이 안되게 된다.
Sigmoid 나 tanh를 사용할 경우, M.L.N.N.은 99%확률로 saturation 된다고 한다.
이 saturation을 막는 방법은 여러가지가 있다.
activation function을 ReLU로 바꾸어도 되고, weight를 다시 초기화해도 된다.
이번시간에 다룰 주제는, Weight initializaiton을 통해 saturation을 막도록 잘 초기화 해보는 것이다.
그렇다면, weight를 초기화하여, activation function에 input되는 z( feature dot product weight)가 saturation 범위에 안걸리도록 하려면 어떻게 해야할까?
sigmoid, tanh를 activation func으로 계속 쓴다고 가정하였을 때,
가장 중요한 요소는 z의 범위( -1 * 100 | +1 * 100 )에서 100을 의미하는 input되는 뉴런(feature)의 개수이다.
만약 neuron의 개수가 100에서 1000개로 늘었다고 가정해보자.
weight2와 dot product 계산시 z의 최소값, 최대값도 10배 늘게 된다. 그만큼 weight범위를 1/10로 줄여야 z의 범위가 유지될 것이다..
이러한 z의 범위를 결정하는데 있어서, input의 neuron의 개수를 고려해서 weight의 초기화 범위를 수정해야한다.
각 모델의 neuron개수가 정해져있다면, weight초기화 범위만 그 neuron수에 맞게 조절하면 될 것이다.
즉, activation func(a)로 들어가는 z의 범위를 -1 과 1사이로 만들어주어 Sigmoid와 tanh의 input범위를 좁히면,
saturation범위에 안걸리게 된다.
이 때, weight 초기화시 범위를 줄이는 방법으로 z의 범위를 줄이는데, 그 기준이 ( 1/ input neuron의 개수 )가 되는 것이다.
input의 neuron의 개수에 따라 weight초기화 범위를 결정 -> z범위 바뀜 -> 시각화시 a로 들어가는 input범위 바뀜 -> saturation 안걸림
각 레이어마다 이러한 현상이 일어날 것이다.
그럼 input의 neuron 개수 뿐만 아니라 output의 neuron개수도 중요해진다.
이러한 두 개념을 전문 용어로 fan in과 fan out이라고 한다.
Fan in (input neuron의 개수) 와 Fan out(output neuron의 개수)
fan in : input Layer의 neuron 개수
fan out : ouput Layer의 neuron 개수
지금까지는 weight초기화시 dot product 계산이 들어가는 forward propagation만 다루었기 때문에, fan in만 고려했지만,
backward propagation에서도 똑같은 현상이 일어나기 때문에 fan out의 개념도 중요하다.
output neuron의 개수(fan out)이 늘어나면 똑같이 back propagation도 늘어나기 때문에, weight 초기화 범위도 그만큼 줄여줘야한다.
이후에 다루도록 하자.
그러면, sigmoid, tanh를 activation func으로 사용하는 모델사용시 weight 초기화를
기존에 사용했던 -1 ~ +1 에다가 fan in(input neuron의 개수)를 나눈 -1 / fan in ~ +1 / fan in 으로 uniform 초기화 해주면 될까?
사실 그렇지 않다. 경험적으로 fan in에다가 루트를 씌워준 값을 나누어주면 더 성능이 좋다고 한다.
그러면 이렇게 초기화한 weight는 M.L.N.N. (Sigmoid)에서 잘 작동할까? 벤치마킹한 결과를 보자.
x축은 epoch이며, y축은 Activation func 의 output값(Activation value)이다.
sigmoid의 경우, 시각화를 생각해서, output값이 0 or 1에 가깝다면 saturation에 걸려 안좋은 상황이다.
[] [] [] [] [] -- hidden Layer가 총 3개 + output Layer 1개에 대해서
a(activation func씌운 output value)를 계속 비교해본 것이다.
빨간색 Layer(Layer1)은 activation output이 평균이 0.5(실선)에 가깝게 나타난다. input(z)는 0에 가깝웠다는 말이 된다.
이 때, 세로바는 a의 표준편차 인데, 0.5에서 왔다갔다한다.
- 우리가 원하는 그림이다. z가 0에서 멀여져 a가 0 or 1으로 갈수록 접선의 기울기가 0이 되는 saturation이 안나와야한다.
Layer가 늘어남에 따라, 초록색Layer -> 파란색Layer -> 검은색 Layer로 갈 수록, 0.5에 가깝던 평균/표준편차가 흔들기리 시작한다.
빨->초->파 순으로 보자. Hideen Layer를 쌓으면서, 평균이 점점 높아진다. 하나 더 쌓으면 평균이 1에 가까워 질 것이다.
output Layer까지 포함하여, 총 3+1 Layer에서 하나의 hidden Layer를 더 쌓게 되면, activation function의 output이 평균 1이 되고, 그곳은 saturation을 일으키게 되는 곳이므로, w의 업데이트가 없어질 것이다.
우리는 Layer가 늘어나더라도, activation value가 saturation되지 않는 곳(sigmoid의 경우, 0.5)에서 평균과 표준편차가 일정하기를 원한다.
sigmoid를 activation func으로 쓰는 모델의 성능을 개선하기 위해 fan in을 루트를 씌워서 나누어, weight를 초기화하는 방식의 문제점은 Layer를 쌓을 수록 잘안되는 느낌이 들면서, Hidden Layer가 3개까진 수렴하나, 4개부터는 train이 안되는 문제점을 발견한 것이다. 그리고 그 이유를 activation value가 일정하지 않기 때문에 발생하는 문제라고 생각했다.
Layer를 늘리더라도, activation value가 평균과 표준편차가 일정하게 유지되도록 weight를 초기화하면 Layer를 무한개 쌓을 수 있다는 이론적 결론을 내릴 수 있다.
종합적으로, input( 이전Layer의 activation value)와
Layer를 늘린 다음층 Layer의 activation value의 평균과 표준편차가 일정해야한다.
아래 그림은, weight initialization을 이상적으로 하여, activation output(value)의 평균(0.5로)과 표준편차가, Layer를 늘리더라도, 항상 이전Layer의 activation의 평균과 표준편차가 일정하게 나온 그래프이다.
어떻게 acitvation value의 평균과 표준편차가 Layer를 쌓더라도 일정하게 할 수 있을까?
현재까지는,
weight -1 ~ +1 --> z의 범위가 a의 saturation범위로 걸림 ->
fan in + 루트 개념을 도입해서 weight 초기화 -> Layer를 늘렸더니 a가 saturation범위로 가까워짐 ->
어떠한 weight 초기화 방법으로 인해 -> Layer를 늘리더라도 이전 Layer의 activation value와 평균과 표준편차가 일정하게 유지 되어야한다.
먼저, 가장 이상적인 경우를 구해보자.
평균과 표준편차가 일치해야한다. 증명에 있어서는 평균과 분산으로 weight초기화 format을 만들어보자.
무한이 많은 Layer가 있다고 가정하며, 그 중 중간의 Hidden Layer 2개만 떼서 생각해보자.
목적은, input X와 output Y (둘다 z에 activation func을 씌운 activation value)의 평균과 분산이 일치하도록 weight 초기화하여, Layer가 늘어나더라도 saturation에 안빠지고 model이 잘 train시키도록 만드는 것이다.
format을 만들기 위해서 몇가지를 가정하는데, X와 Y는 평균0으로서 서로 일치하게 만들어놓는다.
목표는 X와 Y의 분산이 일치하도록 W를 초기화 하는 것이다.
1) W의 평균은 0으로 가정( 초기화시 지정할 수 있다)
2) X와 Y의 평균은 0이라고 가정할 것( 둘다 hidden Layer의 뉴런으로서, activation values다. sigmoid, tanh는 activation value의 평균 0임)
3) 가장 단순한 linear activation function( y =x )를 사용할 것(나중에 튜닝)
- 그 결과 Y(a) = activation function ( z = W*X)에서 --> Y = W*X 가 된다.
이제 W의 평균은 이미 0으로 가정했지만, 분산V(W)를 뭐가나오도록 초기화할지만 고민하면 된다.
여기까지의 결과로서, weight를 잘 초기화하기 위해서는,
1. weight의 범위는 [ -1/ 루트(fan in) ~ +1.0 / 루트(fan in) ]
2. weight의 분산은 [ 1 / ( fan in) ] 이 되어야한다.
그러나, 여기까지는 forward propagation만 고려한 weight 초기화 방법이다.
backward propagation도 고려해야한다. 비슷한 공식이 쓰이나, 설명은 생략한다.
결과적으로 W의 분산은 [ 1 / ( fan out ) ]이 되어야한다.
forward propagation과 backward propagtion을 모두 고려했을 때,
이상적인 weight initialization을 위한, weight의 분산은 아래와 같다.
input neuron의 개수와 output neuron의 개수가 동일하다면, 그냥 1/n을 W초기화시 분산으로 쓰면된다.
다르면, 각각의 합을 더한 것을 2에다가 나누는 조화평균을 쓴다.
결과적으로, 초기화하려는 특정구간의 W에 대해서
앞의 Layer의 neuron 개수 와 뒤 Layer의 neuron개수를 더한 것을 2에 나누면 된다.
이러한 weight초기화 방법을 논문에서는 Normalized initialization, 실무상에서는 Xavior initialization 이라고 한다.
Gaussian 과 Uniform - 실제적으로 쓰이는 Xavior initialization시키는 weight초기화 방식2가지
weight시, 위에서 구한 Xavior initialization을 쓰고싶다면
[ 2/ fan in + fan out ] w의 variance + w의 평균은 0으로 초기화하는 방식을 Gaussian 초기화(평균0, 분산 Xavior지정 w초기화)라고한다.
그리고 w의 범위의 min값, max값을 지정해줘서 균등한 랜덤분포로 초기화하는 방식을 Uniform 초기화(범위지정 균등 w초기화)라고 한다.
uniform 초기화 방식은 min(a) 와 max(b)값을 지정해주면, 그 사이에서 균등하게 랜덤분포를 뽑아내며,
분산은 공식유도상 1/12 * (b-a)^12로 이미 증명되어있따.
Uniform의 분산이 위에서 good weight initialization이 되도록하는 Gaussian의 분산 [ 2 / (fan in + fan out) ]과 동일하게 나오도록 하기 위한 범위(a, b)를 구해보자. 결과적으로 범위는 a,b는 +- 루트( 6 / fan in + fan out)이 되어야한다.
그 과정을 증명해보자.
결과적으로, weight초기화시 Xavior initialization하는 방법 2가지가 있는데,
1. Gaussian 방식으로 w초기화 : 평균0, 분산 : 2 / (fan in + fan out)
2. Uniform 방식으로 w초기화 : min, max를 +/- : 루트 ( 6 / (fan in + fan out) )
이러한 Xavior initialization 으로 weight를 초기화시키는데,
forward / backward 모두 activation value의 평균과 표준편차를 Layer마다 일정하게 유지시켜,
saturation없이 w를 잘 업데이트 시킬 수 있게 된다.
위는 before, 아래는 Xavior initialization로 weight초기화 after이다.
지금 껏, M.L.N.N.의 forward propagation시
어떤 hidden Layer의 activation output의 평균과 표준편차가(Sigmoid or tanh) 모든Layer에서 일정하게 유지되도록 만들어주는 weight초기화 format인 Xavior initialization(분산 : 2/ fan in + fan out or 루트 6/ fan in+ fan out)을 쓰도록 해서
Layer를 쌓을 때마다 평균, 분산(표준편차)가 변하지 않고 일정하게 만들었다.
(before에서는 평균은 0으로 유지되나, 표준편차(분산)의 폭이 좁아지면서 0이 되면, activation output값이 전부 0이 나와버려, 잘못된 결과가 나온다)
여기서 Layer를 더 쌓을수 있어서 성능이 더 좋아질 것이다.(결정적 장점)
backward propagation은 뒤쪽의 Layer의 w변화량(L을 w로 편미분)을 앞쪽 Layer의 w변화량으로 나눈 w변화량의 비율인데, Xavior intialization을 쓰지 않게 되면, forward의 Layer 1->5 처럼, Layer 5->1로 오면서, 평균은 0으로 유지되지만, 표준편차(분산)이 폭이좁아지면서 0이 되어버리면, activation value(output)이 전부 0이 나와버려서, 잘못된 결과 -> Layer를 줄여야한다.
Xavior initialization으로 weight를 잘 초기화하면, Layer를 더 쌓을 수 있지만, 충분한데도 더 쌓지 말 것.
결론
1. 같은 모델이라도 weight 초기화 잘하면 Layer 더 쌓을 수 있어 성능이 좋아진다.
2. weight 초기화 방식은 Gaussian(분산)이든 Uniform(범위)이든 기본적으로 랜덤이지만, fan in과 fan out이 깊게 연관된다.
3. sigmoid나 tanh를 activation func으로 쓸 땐, Xavior(Normaizaed) initialization을 사용하여 weight를 초기화하면, Layer를 더 쌓을 수있다.
4. 그러나 ReLU는 Xavior를 구할 때 쓰던 가정인, X,Y,W의 평균 = 0 중
activation output인 X, Y의 평균이 0이 아니기 때문에 튜닝해야한다.
실습
복습 노트북의...뭐가 수치..가 이상하게 나왔다. solution을 참고해서 다시 해보자.
Keras에서의 weight 초기화 방식
https://keras.io/initializers/
- random_normal : Gaussian분포로서(평균0, Xavior분산적용) -> 평균과 표준편차를 이용해서 weight 초기화
- random_uniform : min, max지정하여 하는 것. 앞으로 잘 안쓰일 것(Small_random_number)
- Othgonal : 자연어 처리시 쓰이는 것
- lecun_uniform : 그냥 루트 씌운 것
- glorot_normal : Xavior initialization by Gaussian 방식
- glorot_uniform : Xavior initialization by Uniform 방식
- he_normal : 케인 he 가 만든 ReLU의 initialization
- he_uniform: 케인 he 가 만든 ReLU의 initialization
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
| 11. Optimization - local optima / plateau / zigzag현상의 등장 (1) | 2018.08.02 |
|---|---|
| 10. transfer learning (0) | 2018.07.31 |
| 8. activation function - saturation현상 / zigzag현상 / ReLU의 등장 (2) | 2018.07.27 |
| 7. Pracical Usage of Convolution Layer - 3,3filter / zero padding/ strides / trade off / 1x1 C. Layer (2) | 2018.07.26 |
| 6. history of Deep Learning (0) | 2018.07.26 |
8. activation function - saturation현상 / zigzag현상 / ReLU의 등장
파이썬 코드로 짠 M.L.N.N.의 코드를 하나하나 살펴보자.
위에는 Multi-Layer Neural Network(fully-connected N.N.)의 prototype이다.
여기서 하나하나의 요소를 개선해서 성능을 높일 수 있다.
activation function-> sigmoid만 썼었다.
weight initialization-> uniform으로 -1~1사이 랜덤하게 줬었다. 그리고 gradient를 태워서 알아서 찾아가게했다.
- 여기서 weight가 2개(행렬 묶음)이라는 것은 Layer가 2개라는 뜻이다.
Optimizer -> gradient descent로 backward propagation으로 w를 업데이트 해줬었다.
오늘은 이 중 activation function에 대해 공부해 볼 것이다.
Activation function
이 activation function은 각 layer에서 나오는 output(a1)을 복잡한 모델로 만들어주는 역할이라 생각하자.

먼저 우리 코드 가운데 sigmoid를 살펴보자. sigmoid는 2가지 역할이 있다.
- activation function으로서, 각층의 Layer마다 들어가서, 모델의 복잡도를 올린다.
- output function으로서, 0~1사이의 값을 가지게하여 classification ( 0 or 1)이 나오도록 하는 squarsh function
- z1까지는 덧셈과 곱셈으로만(linear : 단순함) 이루어져 있었다.
여기에 sigmoid를 씌워(non-linear : 복잡함) 모델을 더 복잡하게 만들어주면 성능을 높일 수 있을 것이다.
여기서 sigmoid는 복잡한 연산이가능케 해주는 Activation function의 역활이다.
여기서 만약에 sigmoid를 안씌운체로, 다음 Layer의 input으로 들어간다면??
아래의 그림과 같이 M.L.N.N.의 마지막Layer의 output(h(x)- y_predict)가 Single-Layer Neural Network수준으로 나오게 되어
복잡한 연산을 하지 못하게 될 것이다.
즉, 중간중간Layer마다 activation function이 들어가지 않아 non-linear하지 않고 linear해진다면,
아무리 Layer를 깊게 쌓는다고 하더라도 결국에는 w1개 + b1개로 학습시킨 것과 마찬가지가 된다.
딥러닝 Layer의 복잡도를 높혀주어야된다!! - 마지막층의 z2에 씌운 sigmoid는 사실 keras상에서도 이름만 Activation function이지,
역활은 input이 뭐가 들어가건 output이 0~1사이의 값이 나오도록 squarshing하여 classification이 가능하게 해주는 Squarsh function이다. 이후 다른 함수들과 같이 output 이라 불린다.
나중에는, output function이 sigmoid 이외에 softmax가 많이 쓰인다.
특히, multi-class classification할 때 많이 쓰인다.
softmax는 output function으로만 쓸 수 있지, activation func을 대체할 순 없다.
결론)
M.L.N.N. (= feed-forward N.N. = fully-connected N.N)의 각 Layer에서 W와 X의 dot product연산 후 or
Convolutional N.N. 의 각 Layer에서 convolution 연산 후
무조건 Acitivation func으로 복잡도를 늘려 층을 늘리는 것을 의미 있게 만들어야한다.
다양한 Activation function의 종류와 장,단점
- Sigmoid
- 장점 : activation func으로서의 장점은 없다. 앞으로는 다른 activation func를 쓰고, 마지막 output function(squarsh func)으로만 쓰자.
- 단점 : activation func의 좌우로 접선의 기울기가 0(da2/dz2)이 되는 지점이 -6, +6만 되어도 시작되어, back propagation을 이용하여 편미분할 때, dL/dw가 0이 되므로 w의 업데이트가 없어지는 saturation현상이 발생한다. (앞으로 나올 모든 activation func의 단점)
뒤쪽의 Layer가 Saturation 되면 앞의 모든 Layer도 Saturation되어 w의 업데이트가 중지된다
.즉, activation func의 시각화했을 때, 접선의 기울기가 0이 되는 지점은 da/dz = 0이 되어
w업데이트량(w=w-람다*dL/dW)을 의미하는 dL/dW도 체인룰로 풀어보면 0이 된다.
이것이 saturation현상이며, sigmoid뿐만 아니라 모든 activation func의 단점으로 작용한다참고)
Loss = Mean Square Error를 쓰는 Regression문제에서,
- L(y,h(x))의 w2편미분 = w와 L(y,h(x))의 시각화시 접선의 기울기 = 0 ===> loss 0인 지점으로 best w찾은 것
Classification문제에서 각 Layer마다 모델복잡도를 위해 씌우는 Activation Func에서,
- a2와 z2로 시각화시, 접선의 기울기 = 0 ===> saturation되는 지점으로 w업데이트량이 0인 지점.
saturation현상이 있는지 판단하고 싶다면, actication function을 시각화 한 뒤, 기울기가 평평해지는 지점이 있는지 보면 된다.
saturation현상을 포함해서 w의 업데이트가 0이 되는 현상을 모두 일컫어 vanishing gradient이라고도 한다.
sigmoid의 activation func으로서 2번째 단점은 squarshing할려고 한 것도 아닌데 계속 sigmoid의 결과값이 0~1사이(+)로 나오게 된다.
그리고 sigmoid의 편미분값(기울기, 0에서 최대 0.25로 가파름)도 0 ~0.25사이(+)로 나오게 된다.
그 결과 아래와 같이 w2의 업데이트량은 하나의 부호(모두 + or 모두 -)로 결정된다.
그러면 이렇게 activationfunc 0~1로 양수 + activation func편미분(시각화시 기울기)도 양수 -> w2업데이트량 부호통일 은
어떤 문제가 생길까?
best의 w를 찾아가는데 있어서, 업데이트량이 항상 같은부호의 matrix로 구성되어,
직선으로( + -> - ) 갈 수없고 (+ -> + , - -> -) 로 움직이는 ZigZag현상이 발생하여 업데이트가 느려진다.즉, sigmoid의 output(0~1) 및 sigmoid의 편미분(기울기, 0~0.025)가 모두 양수이므로
w2의 업데이트량은 언제나 + or -가 나오며, 업데이트 방향을 잡을 때, 비효율적으로 zigzag현상이 발생하여, 업데이트 속도가 느려진다.
사실 best W를 찾아가는 가장 이상적인 activation func, +비중과 -비중이 비슷하면서 saturation안되는 y=x형태의 linear이다.
그러나 activation func이 linear면 Layer를 쌓아도 결국에는 single-Layer수준밖에 안된다는 것을 배웠다.
sigmoid의 세번째 단점은, np.exp연산이 들어가므로 연산이 느리다.
- 사실은 Convolution연산이 더 오래 걸린다.
그래서 이 sigmoid의 단점을 보완하기 위한, 개선된 activation func들을 알아보자.
tanh(hyperbolic tangent) : 탄치
sigmoid와 유사하게 생겼지만, sigmoid의 output 0 ~ 1(양수)
- 장점 : 결과값(output)이 -1 ~1사이면서, (-)와 (+)가 나오는 비중이 비슷하므로 --> zigzag현상이 덜하다.
- 단점 : 변함없이 saturation현상이 있어 w업데이트가 멈출 수 있다. exp연산(4)이 더 많아서 시간이 더 오래걸린다.ReLU(Rectified Linear Unit) : 가장 많이 사용할 activation func, 실제 적용시 효과가 가장 좋다.
- activation func을 넣는 이유는 non-linear한 함수를 씌우는 것인데, non-linear하면서 가장 심플한 함수이기 때문이다.
- 는 0으로 바꾸고, +는 x그대로 사용하는 function
- 장점 : saturation되는 부분이 2군데에서 1군데로 줄었다. / exp연산이 없이 단순하여 빠르다. / loss수렴속도가 sigmoid, tanh에 비해 6배 가까이 빨리 수렴된다.
ReLU가 나오기 전까지는 activation func이 smooth해야 w업데이트가 잘된다고 생각하여 exp연산이 들어간 sigmoid, tanh를 썼었다.
하지만, acitvation func이 smooth한 구간에 걸린 순간, w업데이트 속도가 어마어마하게 느려지는 것이 발견되고,
ReLU의 경우, 편미분(기울기)가 1로 일정하기 때문에, w업데이트 속도가 빨라져 성능이 좋아진 현상이 나타났다.
ReLU가 딥러닝 activation func의 default가 되어버렸다.
- 단점 : ReLU의 output(결과값)이 0 or (+) / ReLU의 편미분 값도 0 or 1(+) --> sigmoid처럼 둘다 양수라서 zigzag현상이 생긴다.
( w2 업데이트의 부호가 항상 같으므로, best w2를 찾아갈 때,,, 지그재그로 간다)결과적으로, saturation은 막을 수 없지만, sigmoid나 tanh보다 접선의기울기가 0되는 부분이 적기 때문에, ReLU를 쓴다.
LReLU, PReLU ( Leacky ReLU, Parametric ReLU)
- ReLU의 업그레이드 버전이나, 성능이 좋다고 100%말할 수 없는 activation func
- 리키 렐루 : x가 음일 때, 0이 아니라 0.01을 곱해준다.
- 파라메트릭 렐루 : x가 음일 때, 0.01이 아니라 알파값을 주고, back propagation / gradient로 w와 같이 train시켜 업데이트한다.
- 둘다 saturation하는 부분(접선의 기울기0)이 없다.
그러나 default는 ReLU만 쓰고, 거기서 성능개선시 바꾼다.ELU ( Exponential Linear Unit) : E렐루
squarsh function(output function)으로 sigmoid이전에 threshold function에 대해서 얘기했었다.
하지만 이 함수를 쓸 수 없는 이유는 output function(squarsh function)이 미분불가하면
Loss func이 smooth하지 못한 상태, 울퉁불퉁한 상태로 정의되기 때문에,
gradient로 w를 업데이트 못시키거나 local optimer가 생길 수 있어서라고 했다.
렐루도 마찬가지로 0에서 미분이 불가하다. 그러나 output function(squarsh function)이 아니므로,
activation func으로는 미분불가해도, 0에 걸릴확률은 적으니 퉁치고 사용했던 것이다.
왠지 미분불가하면 activation func도 사용하면 안될 것 같다 생각하는 사람이 개발한 것이다.
그러나 ReLU보다 딱히 성능이 높아지지 않기 때문에 쓰는 사람만 쓴다.SELU (Scaled Exponential Linear Unit)
- 엘루와 비슷하나, PReLU처럼, 파라미터를 집어넣어 train시킬 수 있게 ELU를 수정한 것이다.
- 알파값 2개를 파라미터로 넣어, train시키면--> activation func의 분산이 일정하게 나와, 성능이 좋아진다고 알려졌다.
그러나, 알파값에 따라 activation func의 결과값이 일정하지 않기 때문에--> Layer를 많이 쌓을 수 없다.
( activation func의 결과값이 일정해야 Layer를 더 많이 쌓을 수 있다. 차후 학습하자)
이것도,, ReLU에 비해 딱히 성능이 많이 좋아지진 않는다.Swish : Google에서 나온 가장 최근의 Activation func
ReLU와 비슷하게 생겼는데, smooth하다.
activation func인데도, 드물게 0근처 음수에서 급하게 꺽였다가 다시 올라가서, 편미분/접선기울기가 음수가 나와서
좀 더 복잡한 activation func으로 성능이 더 좋을 것이라고 예측된다.Maxout : saturation현상과 zigzag현상을 커버하는 유일한 activation func
maxout은 weight를 똑같은 버전으로 2개를 만든 뒤, dot product로 2개를 따로 train하고 난 뒤,
2개의 weight 중 큰 것만 가져와서 activation function으로 쓴다.
dot product의 결과는 linear한것으로만 나오지만, max연산을 통해 non-linear가 된다.
실제 성능도 가장 좋게 나오지만, weight가 2개가 필요하기 때문에, 비효율적이다.정리
weight를 초기화를 잘했다는 가정하에 activation function에 따른 성능을 비교한 그래프이다.
- 파란색 ReLU와 노란색 swish의 성능은 거의 비슷하다.
- 주황색 identity(activation func안쓴것) 과 sigmoid의 성능은 결국 비슷해진다. sigmoid는 초반에 속도가 오히려 더 느리다.
weight초기화를 제대로 못한 경우의 activation func 성능비교를 보자.
- sigmoid가 가장 높은 성능을 보인다.
- 그다음이 relu와 swish는 비슷한 성능을 보인다.
결과적으로, ReLU나 Swish나 비슷하므로 ReLU를 activation function의 default로 쓰자.
더 성능을 뽑아내고 싶다면, 다른 것을 써보자.
activation function은 아직 미지의 영역이다.
요약하자면)
Activation Function을 쓰지 않으면, Layer 더 쌓더라도 의미가 없어질 수 있기 때문에,
Conv Layer나 Fully-connedcted Layer의 연산후에 무조건 activation Function을 입혀주자.
여러가지 activation function이 있지만, 결과적으로 우리는 ReLU를 쓰면 된다.
더 성능을 개선하고 싶다면, 리키렐루, 피렐루, 엘루, 에스엘루, 스위스를 써보면 된다.
궁극의 성능을 뽑고한다면, maxout을 써보자.
sigmoid는 output function(squarsh function)목적으로만 쓰자. 다음에는 softmax를 배워서 쓸 것이다.
실습
python으로 sigmoid, tanh, ReLU를 정해보고, accuracy의 성능을 비교해보자.
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
7. Pracical Usage of Convolution Layer - 3,3filter / zero padding/ strides / trade off / 1x1 C. Layer
저번시간 까지...
저번시간에는 Convolution Filter(or kernel)이 왜 3*3 이 best사이즈인지 몰랐다...
Convolutional Filter의 size ? why (3,3)?
이미지를 C.N.N. 에 집어넣으면, fully-connected N.N.(기본 Single- / Mult-Layer N.N. 혹은 D.N.N.)보다 더 효율적으로 연산할 수 있었다.
효율적이라는 것은 locally-connedced한 이미지의 특성을 살림으로써, 거리상 멀리있는 pixel을 연산할 필요가 없었다.
weight도 모든 input feature에 대해서 하나하나 다 생성된 fully-connected에 비해,
공유된 shared weight가 돌아다니면서 연산하기 때문에 weight양도 효율적인 것을 알 수 있었다.
이 Convolutional N.N.이 실제로는 다양한 방식으로 조합할 수 있다.
세로*가로사이즈는 몇 pixel이 좋으며, 등등이다.
이번에는 그러한 여러 옵션 중에 어느 것이 best option인지 한번 알아보자.
C.N.N.은 세로*가로개념이 생겼고, Filter도 마찬가지였다.
그 중 Convoluation Layer (= Convolutional Filter 의 묶음 )의 best사이즈는 3*3이다. 그 이유에 대해서는 아래를 살펴보자.
14년도 VGGNet과 GoogLeNet의 경쟁이었다. image-net challenge에서 우승은 GoogLeNet이 했지만, 실용적이고 더 연구가 많이 되는 것은 VGGNet이었다. VGGNet의 개념이 나오기 전까지는 Convolutional Filter가 크면 큰 ouput feature를 뽑아내고, 작으면 작은 feature를 뽑아낸다고 생각해왔다. 그러나 이러한 개념을 깬 것이 VGGNet이었다.
VGGNet의 개념은 작은 필터(3*3)을 쓰더라도, Layer를 겹쳐서 여러개의 필터를 거치면, 큰 feature를 뽑아낼 수 있다는 것이다.
즉, 이전까지는 5,5의 큰 input feature는 5,5의 큰 filter 하나만 써야지 외곽pixel들의 관계도 연산이 가능한다고 했었지만,
VGGNet에서는 5,5하나도 가능하지만 3,3Filter를 2개 Layer에 걸쳐 결과적으로 외곽pixel들의 관계도 연산이 된다고 한 것이다.
결론적으로, Convolutional Filter에서는 5,5 Filter 1개나 3,3 Filter의 Layer를 2개 겹쳐서 쓰는 것과 커버하는 영역이 똑같다.
그렇다면 5,5 Filter 1개 쓰는게 좋냐? 3,3 Filter 2개 쓰는게 좋냐? 를 물어본다면 결과적으로 3,3 Filter 2개를 쓰는게 더 좋다.
왜냐하면 weight의 개수와 메모리의 관점에서 5 x 5 Filter의 weight의 개수는 총 25개이다.
3 x3 Filter에서는 weight의 개수가 9개이며 2개를 쓴다면 총 18개의 weight를 가진다.
같은 성능을 낸다면, weight가 적어야지 --> 그만큼 연산량도 작아지고, 메모리 효율도 좋아진다.
결론적으로 Convolutional Filter의 Best 세로*가로는 3*3인 것이다.
저번시간에 ZFNet은 각 C. layer별로 Filter들을 시각화 할 수있다고 하였다.
1번째 Layer의 필터들에서는 대게 선형의 feautre을 뽑아내지만,
2번째 Layer의 필터들에서는 원형의 feature, 그리고 3번째 Layer의 필터들은 디테일한 feature들을 뽑아내는 것을 확인할 수 있다.
즉, Convolutional Layer가 늘어날 수록, 뒤에 있는 Layer가 좀 더 고차원적인 feature를 뽑아내는데,
이것은 5,5 fillter 하나쓰는 것보다, 3,3filter를 2개의 Layer로 연산하는 것이 더 성능이 좋다고 할 수 있는 것이다.
5,5 filter 하나쓰는 것보다 3,3 filter로 2개의 Layer로 겹쳐쓰는 것이
1) weight 더 적어서 --> 메모리효율 높이고, 실행속도 높다
2) 시각화해보니 Layer가 많을 수록 더 고차원적으로 뽑아내니 --> 더 고차원적인 feature를 뽑아낸다.
이것이 VGGNet의 결론이다.
결론 : keras에서도 Conv2D의 kernel에 (3,3)을 입력해주면 된다.
Convolution 연산의 단점과 극복방안 : zero padding
convolution연산의 단점은 1,1 연산을 하지 않는 이상, input feature의 size보다 output feature의 size가 작아진다는 것이다.
계속 convolution연산하다보면, 계속 작아지니까 결국 연산이 불가능해지지 않을까 걱정될 수도 있다.
이 때, input과 output의 size를 맞춰주는 것이 zero padding이다.
input의 외곽쪽에다가 모두 0인 padding을 1pixel씩 씌워준다.
input5,5를 3,3 convolution연산하게 되면 output이 3,3으로 작아졌었다. 하지만, 5,5에다가 zero padding을 씌우는 순간
3,3 filter가 가로방향으로 3번만 연산할 수 있었던 것이 5번이 가능해진다.
결과적으로 output이 3,3이 아니라 5,5가 된다.
input과 output의 size를 맞춰주기 위해서는 zero paading을 씌면 되는 것이다.
그 결과 더 작아져서 못쌓았던 Layer를 더 쌓을 수 있게 된다.
실제로 keras에서 사용하기 위해서는 Conv2D( Convolutional Layer)의 옵션으로 padding =인자에 옵션을 넣어주면 된다.
이 때, 2가지 옵션이 있는데, 'same'과 'valid'다. padding='same'옵션이 zero padding이니 이것만 사용하면 된다.
Convolutional Layer를 추가할 때마다 추가해줘야한다.
- Convolutional Layer를 넣는데, filter수 = output_filter_size= output feature의 개수는 64로 지정
- kernel_size = filter의 세로가로사이즈 (3,3)으로 best고정
- padding='same'으로 zeropadding씌움 (layer마다 게속 지정해줘야한다)
이 때, zero padding의 부가효과로서, 최외곽(좌상단 or 우하단 등)에 위치한 중요 feature에 대해서, zero padding으로 연산횟수가 늘어남에 따라 여러번 연산이 되어이 뽑힐 가능성이 높아질 것이다 .
즉, 어떤 이미지에서 중요feature가 외곽쪽에 위치하고 있을 때, 그것을 찾을 확률이 높아진다.
좀 더 좋은 효과가 있지만, 그렇게 큰 효과가 있진 않다.(왜냐하면 중요
결론2 : keras에서도 Conv2D의 kernel에 (3,3)을 + padding='same'을 넣어주면 된다.
strides - Filter가 움직일 때, 몇칸씩 뛰면서 움직이냐? (Pooling의 경우 자기 크기만큼 strides)
Filter는 왼쪽에서 오른쪽 / 위에서 아래로 sliding window를 한다고 했다. 보통은 1pixel씩 움직인다고 했다.
만약, 1칸 뛰던 것을 2칸 뛰게 된다면, 연산이 그만큼 줄어들어서, 좀 더 디테일한 feature를 뽑아낼 수 없게 된다.
그러므로 Convolutional Layer 속 Filter의 strides는 1이 best이다. 그래야 촘촘하게 연산할 수 있다.
우리가 keras를 사용하면서 strides 옵션을 줄 때, 1만 주면 된다.
예외적으로 strides 2를 주는 경우가 있다. 바로 Max Pooling을 대체할 때 쓴다.
실무, 연구쪽에서는 맥스풀링을 안쓰려고 하는 경향이 있다.
왜냐하면 Filter의 strides를 2칸씩 뛰면, 연산횟수가 줄어드는데 ( Filter 2,2일때 정확히 반으로 줌) 맥스풀링을 대체할 수 있다.
그런데, 맥스풀링 대신 Conv2D를 사용하면,
장점) Conv Layer의 strides1로 추가하는 것보다는 연산횟수는 줄어드는 반면에
Maxpooling보다 좀 더 디테일하게 feature를 뽑아냄
단점) 맥스풀링을 버리는 입장에서는,없던 Conv Layer추가로인해 그만큼 filter가 생겨나 weight의 전체 수도 증가해버린다.
맥스풀링은 필요없는 feature를 버리는 개념이었다. 예를 들어서, 고양이로 분류하는 문제에서는 고양이의 귀나 꼬리모양 등이 중요feature이고 대부분은 필요없는 feature로서 작용하기 때문에, 더 효율적일 수 있다.
그러나 다른 예를 들어보자.
이미지를 집어넣고, 유사한 고양이를 생성하는 이미지 generation문제에서는 맥스풀링이 문제가 될 수 있다.
예를 들어서, 고양이의 중요feature는 아니지만, 털같은 디테일한 것까지 버려버리면, 고양이와 유사한 이미지를 generate못하게 된다.
즉, 이미지를 제네레이터하는 문제에서는 필요없다고 feature를 버리는 개념은 말이 안될 수 있는 것이다.
결론적으로, 이미지 제네레이터문제에서는 MaxPooling대신 Conv2D의 stride(2,2)옵션으로 해야한다.
결론3 :
Conv2D의 kernel에 (3,3)을 + padding='same' + strides(1,1)을 넣어주자.
이미지를 분류할 때는, 맥스풀링을 써도 되지만 /
이미지 생성할때만, 맥스풀링 금지 -> strides(2,2)인 Conv2D로 대체하자.
Trade off - C. filter를 늘리느냐? 아니면 C. Layer를 늘리느냐?
하드웨어(리소스)가 제한적이기 때문에, 무한정으로 filter나 Layer를 늘릴 수 없다. 이 때, trade off가 필요하다.
결과적으로 Layer를 깊게 쌓는 것보다, 적당한 Layer를 쌓은 상태에서는 Filter를 더 늘리는 것이 더 좋을 수 있다.
152개의 Layer를 가진 ResNet보다 50개의 Layer + Filter수를 늘린 Wide ResNet이 성능이 좋았다는 결과 때문이다.
결과적으로, 어떤 base모델이 있다고 가정하면, Layer를 1/2로 줄이는 한이 있더라도 Filter수를 2배더 가져가는 것이 더 성능이 좋아진다.
결론4 :
Conv2D로 Convolutional Layer를 짤 때,
kernel에 (3,3) + padding='same' + strides(1,1) + Layer를 줄이더라도 Filter를 늘리는 전략
이미지를 분류할 때는, 맥스풀링을 써도 되지만 / 이미지 생성할때만, 맥스풀링 금지 -> strides(2,2)인 Conv2D로 대체하자.
1X1 (Filter를 가진 ) Convolutional Layer 의 3가지 장점
이미지는 기본적으로 locally-connected라는 현상이 있다. 하나의 픽셀이 주변 픽셀과의 연관관계로 feature를 뽑아낸다고 했다.
이러한 locally-connected현상을 연산하는데 안성맞춤인 N.N.가 바로 Convolutional Layer이다. 왜냐하면 똑같이 주변픽셀과 연산을 하므로
예를 들어, 3,3 C. layer는 각 필터들이, 3,3 중 가운데 1 pixel <-> 주변 8 pixel과의 관계를 연산한다.
그런면에서 보면, 1,1 Convolutional Layer은 필요없는 것 같아보인다.
주변픽셀과 연산을 하지 않으므로, 일반적으로 우리가 생각하는 Convolution연산과는 거리가 있다.
이러한 1 X 1 Convolution 연산은 어떤 곳에 쓰일까?
먼저, 딥러닝모델이 설정된 상황에서, 특정 Conv Layer에 (3,3) filter의 사이즈가 64라고 가정해보자.
여기에 bottle neck을 써볼 것이다.
1. 먼저, input 되는 filter size( 이전 Layer의 output filter개수)를 기존 것(64)의 4배를 늘린다.
( 참고 : 이전레이어의 output filter개수 = input되는 filter_size -> 그것과 동일한 input_filer_size의 filter가 연산후 1로 나옴
- > 1로 연산된 filter들의 총 개수 = output filter_size = Conv. Layer)
여기까지 다합치면 C. Layer)
2. input_filter_size를 4배 늘어난 256로 맞춰서 연산이 되도록해주고
(1,1)filter로 연산하는데, output filter( 1로 연산된 filter들의 총 개수)를 다시 64로 넣어준다.
3. 그다음 C. layer에서는 (3,3)filter으로 연산하도록 하고, output_filter의 갯수를 64개로 넣어준다.
4. 다시 마지막 C. layer (1,1)filter로 output_filter가 256개로 넣어준다.
Bottle neck 전략이란?
1. 256개의 input filter를 64개가 나오도록 (1,1)Filter로 압축(encoding)시킨다(임의로 64개 필터로 조정)
2. 중간에서 (3,3)연산해준다.
3. 마지막에 64개의 input filter가 256개가 나오도록 (1,1)Filter로 뿔려(decoding)시킨다.(임으로 256개 필터로 조정)
> 그림의 왼쪽모델에 비해, (1,1) filter를 이용한 Conv. Layer의 bottle neck 전략은
input_filter를 4배 더 많이 넣을 수 있다. & 연산도 더 효율적이다(weight갯수가 더 작다.)
참고 Conv.Layer weight개수 = input_filter_size(64) * filter size( 3*3) * output_filter_size(64)
shared filter는 (3,3)으로 총 3*3 = 9개이다. 그리고 그 필터개수인 output_filter_size를 곱해준다.
3*3 = 9 * 64
여기서 input_filter_size(intput feature의 갯수라 생각)마다 이 필터가 연산을 하므로,
64개의 각각의 input feature에 대해서
9개의 shared feature가 하나의 필터당 weight갯수고
그 필터가 총 64개(output filter_size)있으니
64* 3*3 * 64개이다.
64*3*3*64 + 64*3*3*64 = weight 73,728 개
>> 256*1*1*64 + 64*3*3*64 + 64*1*1*256 = weight69,632개
2번째 (1,1) Conv 연산의 장점은 fully-connected를 대체할 수 있다는 점이다.
아래는 VGGNet 모델이며, 마지막에는 fully-connected로 계산하는 부분이 있다.
이 VGGNet의 마지막 Conv. Layer에서 --> Fully-connected Layer로 넘어갈 때, output되는 weight수가 순식간에 늘어난다.
VGG모델에서는
앞의 모든 Conv Layer를 다 합친 weight의 수보다 << 첫번째 Fully-connected Layer의 weight가 더 많다.
그래서, 4096짜리 FC layer 대신에 (1,1) Conv Layer로 대체하고 output_filter개수만 4096개로 조정해주면 된다.
input필터의 개수가 512개이므로, output filter 개수는 4096개로, 총 weight개수는 (1*1*512*4096)개 이지만,
FC Layer의 weight개수(7,7,512, 4096)보다 적다.
그래서 FC layer를 (1,1)Conv Layer로 대체하고, weight줄어든 만큼 filter를 늘리거나 layer를 더 쌓는 trade off를 할 수 있다.
마지막 장점은 Dense전략으로서,
fully-connected N.N. = M.L.N.N. 는 input 이미지의 size가 정확히 모델과 일치해야하는 단점을 가지고 있었다.
(MNIST 28*28=784가 정확히 일치해야 들어간다)
그러나 Conv. Layer는 input사이즈는 딱히 중요하지 않다.
대신 input이미지의 사이즈가 줄면 filter를 거쳐 output이미지의 사이즈가 더 줄어들 뿐이다.
VGG모델은 보통 세로*가로 (244, 244) 이미지가 들어간다.
만약 full-connected라면 정확히 244*244 이미지를 안넣어주면--> Conv Layer까지는 연산이 되지만,
정해진 사이즈가 안들어와서 정해진 input이 안들어온 Fully-connected Layer에서는 에러가 날 것이다.
Conv Layer는 인풋이미지의 사이즈와 상관없이 연산이 쭈욱 일어난다. 다만, output사이즈만 달라질 것이다.
예를 들어, train할 때 Fully-connected Layer를 (1,1)Conv L.로 대체했다고 해보자.
input을 (14,14) 로 넣고 (5,5)Conv (10,10 ) -> (2,2) Pooling (5,5) -> (5,5)Conv (1,1) -> (1,1)Conv (1,1)Conv (1,1)Conv -> (1,1)
으로 output (1,1)이 하나 생겨 이것을 가지고 고양인지 개인지 구분할 것이다.
만약 이미지사이즈를 키워서 input을 (16,16)으로 넣어줬다면??
-> 마지막이 Fully-connected였다면 마지막에 에러가 날 것이다.
-> 마지막을 (1,1)Conv Layer로 대체했다면? 에러없이 output이 (2,2)로 좀 더 커질 뿐이다.
AlexNet에서는
이미지(224,224)를 정확한 하나를 넣어주는 것보다.
이미지를 argumentation하여
1) 사이즈를 약간 키워준 뒤,(224,244->256,256)
2) 다시 좌상단 + 우상단 + 좌하단 + 우하단 + 가운데(244,224) 로 Crop한 뒤
5) 5개의 (224,224)를 좌/우반전 시켜 총 10개(224, 224) 넣어주는게 더 성능이 좋았다고 했다.
> 1개가 10개가 되니, test할 때,속도가 10배가 느려지는 단점이 있다.
> 그럴바에는 조금 더 큰 이미지가 들어갈 수 있게
FC Layer -> (1,1) Conv Layer로 대체하고 + 약간 큰 사이즈의 이미지를 넣어주어서,
5개크롭/좌우반전한 효과대신 sliding window방식으로 연산한 결과가 더 좋다.
output사이즈가 좀 더 크게 나온 것은 평균내면 된다.
그러면 (224, 224)원본이미지 맞춰서 넣는 거보다 (256,256)좀더 큰이미지를 넣은다음 평균내는게 더 성능이 더 좋다.
결론 : (1,1) Conv Layer를 쓰는 장점 3가지
1. bottle neck전략 : (3,3) Conv L. 2개쓰는 것보다 (1,1)encoding (3,3) (1,1)decoding Conv. Layer 3개 쓰는 것이 성능이 더 좋다.
2. fully-connected L. 를 (1,1)Conv. Layer로 대체하면 weight수가 줄어 메모리 효율적
3. fully-connected L. 전부 (1,1)Conv. Layer로 대체하면, input이미지의 사이즈가 자유로워져 ->
(train시에는 모델에 맞는 input이미지 크기로 학습)
test시에 좀 더 큰 이미지를 넣어 (2,2)결과가 나온 것을 평균내주면, 똑같은 train모델에 대해서 더 좋은 성능을 가진다.
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
6. history of Deep Learning
딥러닝
딥러닝 자체는 트렌트적 용어이다.
비교해볼 블로그 : http://nmhkahn.github.io/Casestudy-CNN
1957년에 시작하여 1960 ~1970년, 인공지능의 황금기(Golden Age)
딥러닝의 초안은 Perceptron 알고리즘이며, 인공지능의 부흥을 가져온 알고리즘이다.
이 당시 연구자들이 모이면서, 연구자들이 모이는 황금기가 찾아왔다.
그러면서, 2가지 학파가 생겼다. 연결주의 학파와 기호주의 학파이다.
딥러닝에 대한 인공신경망을 개발한 곳은 연결주의 학파이며, 너무 부흥하다보니까 기호주의 학파는 제대로 살아갈 수 없었다. 그 결과 연결주의 학파의 perceptron의 한계점을 지적하여 비판하기 시작하였다.
1970 ~ 1980년, 인공지능의 암흑기 (Ai winter)
그 비판의 핵심은 아주 간단한 문제인 XOR problem을 풀지못하는 한계를 지적한 것이다.(저번시간 학습했었다). 그러면서 책을 발간하는데, 연결주의 학파의 perceptron이라는 명칭으로 책을 내버린 것이다. 간단한 문제도 못푸는 주제에 사람을 어떻게 대체할 수 있겠느냐는 내용이었다.
그 결과 연결주의 학파가 망해가는데, 기호주의 학파도 같이 망해버렸다. 같은 인공지능에 대한 학파이기 때문인 것 같다. 이러한 시기를
AI winter라고 하며, 인공지능의 Dark Age(암흑기)가 찾아온것 이다.
1986년, 인공지능 암흑기의 끝, Backpropagation
암흑기를 맞이하게 한 주인공인 XOR problem을 제대로 푸는데 17년 정도 걸렸다. 즉, 암흑기 17년 동안 인공지능 연구가 제대로 되지 않고 있었다.
그러다가 실용적으로 XOR problem을 풀 수 있게한 알고리즘인 Back Proapgation이 등장하였다.
이러한 방식을 채용한 것이 Multi-Layer neural Network(Multi-Layer perceptron)인 것이다.
이 알고리즘을 제시한 유명한 학자들 가운데 가장 유명한 인물이 G. Hinton(제프리 힌턴)이다.
제프리 힌튼(Geoffrey Hinton·68, 토론토대 교수) 은 현대 딥러닝 알고리즘을 거의 다 만들었다.
그 밑의 제자들도 매우 유명하다.
facebook에서 Ai 연구총괄하는 yann lecun 얀 레쿤(Yann Lecun·55) 뉴욕대 교수 -> 페이스북 Ai 총괄)
apple에서 Ai 연구총괄하는 Ruslan Salakhutdinov(러슬란 살라쿠트디노브)
추가적으로 18년도에 영입된 존 지아난드레아(John Giannandrea, 53)
코세라 강의로 유명한 앤드류 응(Andrew Ng·39, 스탠포드대 교수)
1995년, SVM의 개발
SVM은 코어의 갯수와 무관하게, 분산처리가 안된다는 한계점을 가지고 있다.
그러므로 스몰데이터에서만 먹히게 되었다. 그 결과 사장되기 시작했다.
2006년부터 2010~ 딥러닝 부흥기
딥러닝이란 용어가 본격적으로 사용되는 것은 2006년, 제프리 힌튼과 그의 제자 러슬란이 RBM(restricted Boltzmann machine)이라는 볼트만 머신을 만들면서 였다. 러슬란이 힌튼의 박사과정을 진행하는 과정 중, 힌튼이 오버피팅을 방지하는 방법을 제안하면서 본격적으로 사용되었다고 한다.
참고로 2013년도 신호처리학회 (ICASSP)에 의해 고안된 Dropout으로 인해 오버피팅을 효과적으로 배제할 수 있게 된다.
부활한 인공신경망과 음성인식
딥러닝이 가장 먼저 두각을 드러낸 곳은 음성인식 분야였다. 그 가운데 Switchboard라는 음성 데이터셋이 큰 역할을 하였다.
이렇게 먼저 두각을 보인 이유는, 딥러닝에 있어서 필요한 3가지 조건을 모두 갖추고 있었기 때문이다.
- 좋은 알고리즘
- 양질의 데이터
- 컴퓨터 성능
2000년 후반대에, 양질이면서 대량의 데이터를 갖춘 것, 음성데이터였기 때문이다.
어떤 주제에 대한 음성내용과 그것을 텍스트로 만든 데이터셋이 바로 Switchboard라는 데이터셋이다.
그 결과 Speech to Text가 가능한 상황이므로, 그 가운데의 알고리즘을 연구하게 된 것이다.
힌튼 교수가 있던 토론대에서 이러한 연구를 하게 되고, 큰 성과를 내게 된다.
힌튼 교수의 딥러닝 알고리즘은 사용했더니 Speech to Text의 error가 확 줄게 된 것이다.
이 과정에서 마이크로소프트의 알고리즘을 힌튼 제자들이 인턴으로 가서, 기존이 알고리즘을 격파하고 왔다는 후문이 있다.
부활한 인공신경망과 이미지 인식
음성데이터에 있어서, 스탠포드 대학에서는 1억4천만개의 이미지에 대해서 22000개의 카테고리로 나누어놓은 이미지데이터셋을 만들었다.
압축했을 때 60기가 되는 대량의 이미지데이터셋을 IMAGE NET이라 이름하였다.
그결과 IMAGE to CLassification 알고리즘 연구가 가능해지게 된 것이다.
활발한 연구를 위해, 이러한 분류 알고리즘의 경진대회를 이미지넷 챌린지라고 하여, 년도별로 우수한 알고리즘이 나오기 시작했다.
그리고 2012년부터, 다른 알고리즘과 엄청난 격차를 벌리면서 딥러닝이 다시 한번 유명해지기 시작했다.
2012년, Alex Krizhevsky의 AlexNet
포스트닥터 과정 중이었던 Alex Krizhevsky가 AlexNet으로 1등을 차지하였다.
그 이전까지 IMAGENET 데이터셋의 image classification error rate는 2010(28.2%), 2011(25.8%)로
20대 중후반 %였다.
딥러닝인 AlexNet의 등장으로 음성인식, 이미지분류의 모든 알고리즘의 도장을 깨버리기 시작하게 된 것이다.
- AlexNet의 정리
- 2012년, error rate : 16.4% (확 낮아지는 계기)
- 8 Layers
2013년, 뉴욕대의 ZFNet
AlexNet에 비해 엄청 우수한 알고리즘이기 보다는, 약간 튜닝한 정도의 딥러닝 알고리즘이라고 한다.
- ZFNet의 정리
- 2013년, error rate : 11.7
- 8 Layers
2014년, 구글의 GoogleNet 과 옥스퍼드대의 VGGnet
2014년의 이미지넷 챌린지는 구글의 GoogleNet이 우승하였지만, 2등을 차지한 옥스퍼드대의 VGGnet이다.
GoogleNet에 비해 효율이 좋아, 많은 사람들이 이용가능한 딥러닝 알고리즘이었기 때문이다.
- GoogleNet의 정리
- 2014년, error rate : 6.7%
- 22 Layers
- VGGNet의 정리
- 2014년, error rate : 7.3%
- 19 Layers
2015년, 마이크로소프트 리서치(중국)의 ResNet
마이크로스프트의 자체 개발 알고리즘이기보다는, 중국의 마이크로소프트 리서치 회사에서 개발한 알고리즘이다.
이 ResNet을 만든 케이밍 해(Kaiming He)는 스타가 되어, 페이스북으로 영입되었다.
- ResNet의 정리
- 2015년, error rate : 3.57%
- 152 Layers
이미지 인식 알고리즘의 변천사
- LeNet5 (1998), 얀 리쿤(Lecun Y.)
- CNN 알고리즘의 시초, MNIST 데이터셋을 만들기도 한 장본인인 얀 리쿤에 의해 개발
- 지금은 28*28 사이즈를 많이 사용하지만, 당시에는 32*32 사이즈를 집어넣었다.
- 32-> Conv -> MaxPooling -> C -> P -> Flatten() -> FC1 -> FC2 -> FC3(output) = 10
- 옵티마이져로는 SGD(Stochastic Gradient Descent)를 사용
- epoch 20, learing rate를 고정시키지 않고 0.000 5->2->05->01 로 초반에 lr는 크게, loss수렴시 lr를 줄임 -> 반복
- 벤치마킹 결과 ( 정확도-error rate 와 메모리사용량)
-정확도에 있어서, SVM(1%)에 비해 큰 차이는 없었다. LeNet(0.8%)
-SVM과의 가장 큰 차이점은 메모리 사용량이다.
28000->60 - 에러율은 0.8%이므로, 10000개의 데이터 중에 81개만 틀렸다고 볼 수 있다.
[논문용] 하지만, 이 틀린 것들이 틀렸지만 틀린게 아니다라는 것을 강조하기 위해, 아래 그림을 제시하였다.
즉, 틀린 것은 사람의 눈으로도 분류할 수 없다는 것을 강조하였다. - AlexNet(2012), Alex krizhevsky
- 2012년, error rate : 16.4% (확 낮아지는 계기)
- 8 Layers
- 지금부터는 이미지넷 챌린지 우승모델, 인공지능 혁명을 일으킨 최초의 모델, 논문인용이 10000단위
- AlexNet에서 최초로 GPU를 사용(2개)하였다. 당시에는 tensorflow가 없었으므로, cuda라는 것으로 수동으로 분산시켰다.
- tensorflow, pytorch, keras는 알아서 처리해주니, 넣기만 하면 된다. - 논문의 figure상에는 224*224 사이즈로 나왔지만, 실제 구현하려면 227*227을 input으로입력해야한다.
- 첫 Conv는 필터크기가 11*11이며, output은 96개의 필터, stride 4칸 뜀
- 나중에는 stride를 1이 best이지만, 이 당시는 몰랐다고 한다. - 첫 Conv는 Pad 0은 제로패딩을 사용하였다.
- Conv의 단점이, input size와 output size가 작아진다는 것인데, 제로패딩을 넣으면, output size를 input과 동일하게 유지할 수 있다. 당시에는 이 개념없이 그냥 사용한 것이라고 한다. - 첫 MaxPooling은 3*3을 2칸씩 stride하였다. 이 때 크기가 3인 창을 2칸만 뛰므로, 다음 맥스풀링 연산과 1칸이 겹치게 된다.
이러한 방법을 Overwrapped Pooling이라고 하는데, AlexNet에서는 이 오버랩드 풀링을 써서 성능이 향상되었다고 기술했다.
- Max Pooling은 2*2를 2칸씩 뛰어 input size의 크기를 정확히 절반으로 줄일 수 있다. - Norm1은 Conv Layer에 대한 Contrast enchancement process로서, Local response Normalization Layer라고 하는데, 지금은 필요없는 것으로 판명되었다.
- weight initiation에 있어서는, Gaussian 분포를 이용해 평균0, 표준편차 0.01로 초기화하였다.
- activation function으로서의 sigmoid를 ReLU로 바꾸었다.
- Dropout을 사용하여, FC층에서 train시 하나의hidden layer에 있어서, neuron을 전부다 사용하지 않고 0.5rate를 주어 절반만 사용하도록 하였다.
- 딥러닝에서는 고양이를 인식할 때, 꼬리 30% 털에 5%, 귀 15% 얼굴에 50% 이런식으로 확률을 배정한다.
하지만, 커튼에 가려진 고양이의 경우, 꼬리만 보이므로 30%의 확률로 밖에 인식못하게 된다.
그러나, 사람의 경우 꼬리만 보고도 맞출 수 있다.
사람의 인식방식을 모방하여, 꼬리만 보고도 100% 고양이으로 맞출 수 있게,
강제로 neuron의 절반을 지운체 train시킨다.
고양이를 label을 준 상태에서 꼬리, 털, 귀, 얼굴을 랜덤하게 지운체로 weight를 back propagation을 통해 training시키면,
각 부위의 feature가 랜덤하게 지워지더라도 고양이라는 것을 맞출 수 있도록 train되는 것이다.
즉, 강제로 고양이 부위의 일부를 빼놓고 학습시킨다는 것이다. - Batch size는 128장 씩 넣었다.
- 이미지넷 데이터셋은 너무 많으므로,
쪼개서 128장씩 집어넣은 상태에서 foward/backward propage->weight 업데이트 시킨뒤,
다시 128을 가져와 weight를 업데이트 시키는 는 방식이다. - Optimizer는 LeNet5와 동일하게 Gradient Descend방식인 SGD를 썼으나, 추가적으로 Momentum이라는 가속도를 0.9로 주었다.
Weight Decay라는 방식도 이용해서 SGD를 사용하였다. - Learning rate는 0.01로 시작한 뒤, loss가 안떨어질때마다 1/10씩 총 3번 감소시켰다.
- 똑같은 AlexNet을 7개 만들어놓고, 각 7개 모델이 weight 초기화에 따라 미묘하게 달라지는 결과를 평균내는 앙상블(Ensemble)을 사용하였다.
- GPU를 최초로 사용하며 2개를 라이브러리가 없는 상태에서, cuda로 직접 나눠서 분산처리하였다.
- Data Augmentation을 굉장히 많이 사용하였다.
- 좌우반전은 사진데이터에서 필수
- 최초 원본이미지를 256*256*을 만들어놓고, crop을 랜덤하게 224*224로 2048개 만들어서 여러데이터를 넣었다.
Dropout처럼, feature가 일부분 짤리는 효과가 생겨 성능이 올라간다.
- test할 시에는 256*256 를 좌상단/우상단/가운데/좌하단/우하단 5개로 224*224 crop 한 뒤, 각각을 좌우반전하여
총 10배로 데이터를 부풀렸다. - 마지막으로, PCA(Principal component analysis)를 통해 RGB채널을 조정해서 넣어주었지만 현재는 쓰지 않는다.
- AlexNet의 성과로서, 2011년도에 우승한 알고리즘인 Xerox에 비해 딥러닝 알고리즘을 통해 error rate가 상당히 줄어들었다.
그결과 딥러닝의 붐이 일어나기 시작한다. - [논문용] AlexNet은 16.8%의 에러에 대해서, 틀린 그림의 top5를 제시하면서, 비록 틀렸지만, 나머지 4개를 보면 답이 있으며, 사람도 해깔린다 + AlexNet이 제시한 오답도 나름의 이유가 있다는 것을 설명하였다.
예를 들어, 2번째 줄 1번, 2번 그림들은, 오답으로 grile 과 mushroom을 내어노았지만 2번째 답으로 예측하였으며, 비록 1번째 답이라고 보아도 무방함을 나타내었다.
그리고 3번째 그림은 체리 뒤에 달마시안이 있으므로, 사람이 봐도 답을 체리가 아닌 달마시안으로도 낼 수 있다.
4번째 그림은, 사람도 모르는 것인데, AlexNet정도면 잘한것 아니냐는 늬앙스를 심어두었다. - ZFNet(2013년, 뉴욕대), Zeiler & Fergus
- 8 Layers, error rate : 14.8%
- ZFNet은 AlexNet을 튜닝하여 약간의 성능개선이 있었으며, 이미지 챌린지에서의 연구적 가치는 크지 않다.
- AlexNet의 Conv1의 필터 크기를 11*11 -> 7*7로 줄이고, stride를 4->2로 줄였다.
- 3,4,5번째 Conv Layer의 필터수(depth)가 384, 384, 256개에서 -> 512, 1024, 512로 늘어났다. - ZFNet의 눈 여겨볼 사항은 Conv Layer를 시각화 했다는 것이다.
- GoogleNet(2014년, 구글), InceptionNet이라는 이명
- 2014년, error rate : 6.7%
- 22 Layers
- 어머어마하게 복잡한 구조로 Layer를 쌓아놓고 우승하였다. 대기업 자본의 승리라는 말까지 나왔었다.
- 성능이 ZFNet보다 비약적으로 증가하였다 (14.8% -> 6.7%)
- InceptionNet은 Inception모듈에서 나왔다. 비슷한 ConvLayer들이 옆으로 묶여있는 구조를 가진 모듈이다
이러한 Inception모듈을 여러개 묶어놓은 것이 GoogleNet이 되는 것이다
- 당시 유행했던 인셉션 영화에서 디카프리오의 ' 더 깊게 들어가야한다'라는 대사에서 따왔다는 말이다 있다. - 여기서 하나의 14년도의 논란거리가 있다. Conv Layer의 필터 크기가 어느것이 best인지에 대한 논쟁이다.
당시에는 전통적으로 필터가 크면 큰 featuremap을, 필터가 작으면 작은 featuremap을 뽑아낸다는 것이 관례였다.
그래서 구글넷은 어느 featuremap이 좋은 것인지 모르는 상태였기 때문에, 종류별로(1*1, 3*3, 5*5) 필터를 여러개 묶어놓은 inception구조를 택한 것이다. 그리고 나서 딥러닝 알고리즘이 알아서 choice하도록 한 것이다. 이것이 인셉션의 기본 원리이다 - 왼쪽의 Prototype과 달리, 오른쪽은 기존 inception구조에 1*1 Conv Layer가 들어갔다.
이것은 기본적으로 Conv Layer의 의미가 없다. Conv Layer의 핵심은 필터크기만큼의 주변픽셀과 연관관계를 연산하는 것이 핵심이기 때문이다. 하지만, 1*1은 주변픽셀과 연관관계가 없다. 다른용도로 쓰인다. - VGGNet(2014년 2등, 옥스퍼드대)
- 2014년, error rate : 7.3%
- 19 Layers
- VGGNet이 2014년 2등을 했음에도 주목받은 이유[논문용]
1. 알고리즘이 엄청 쉽다.
2. 복잡한 구조의 GoogleNet에 비해, 같은 앙상블시 error차이가 거의 없었다.
3. 앙상블 안한 SingleModel로는 VGGNet이 더 성능이 좋다.
4. Conv 필터의 크기에 대해서, 명쾌한 답변을 하였다.
즉, 서로간의 연관관계를 계산할 수 있는 한도내에서 크기가 작을 수록 작다.고 하였다.
- Conv 필터의 크기는 무조건 홀수로 한다(짝수일 때는, 연산이 잘 안된다)
- 홀수로서, 연관관계를 계산하지못하는 1*1을 제외하고, 가장 좋은 필터크기로서 3*3을 채택하였다.
이 최적의 필터크기인 3*3으로서, 최대한 깊게(depth=필터 수) 쌓을 수록 성능이 올라간다.
5. Layer를 어떻게 쌓느냐에 대한 것에 명쾌한 답변으로, 여러가지모델을 사용해서 테스트하였다.
- A모델(11 Layers)을 만든 뒤, AlexNet에서 썼던 Local Response Normalization Layer를 추가해줬더니 성능변화가 없었다.
- B모델로서, A모델에 필터수 64개, 128개인 ConvLayer를 2개 추가했더니 성능이 좋아졌다.
- C모델로서, B모델에 256, 512, 512를 3개 추가했더니 성능이 좋아졌다.
- D모델로서, C모델에 똑같이 256, 512, 512를 3개 추가해줬더니 성능이 좋아졌다.
- E모델로서, D모델에 256, 512, 512를 3개 추가해줬더니 성능변화가 거의 없었다.
==> 결과적으로 같은성능을 내면서 메모리사용량이 적은 D모델이 최적의 모델로서 선택되었다. (VGG16) - 결과적으로 Conv Layer의 필터크기는 언제나 3*3으로, stride 1칸씩, 1개의 zeropadding을 쓴다.
기본적으로 시작 필터수(output filter size)는 64개로 시작한다. 그 뒤로 2배로 늘어난다(병렬처리 잇슈때문에 선택됨)
구글넷에서 썼던 1*1 conv 는 VGG에서는 효과를 못봤다.(하지만, 나중에 효과를 보여주니 알아야한다)
MaxPooling은 언제나 2*2, strides 2칸씩 뛰어, feautremap의 크기를 절반으로 만든다.
Dropout은 FC layers에만 적용시키며, rate는 0.5로 준다. - 다른 옵션들로서,
Optimizer는 AlexNet과 동일하게, SGD를 사용했으나, 시작 Learning rate 는 10배 늘린 0.1로 시작한다.
하지만 AlexNet과 마찬가지로, error 가 줄지 않을 때마다 1/10씩 줄이는 것을 3번 반복한다.
Momentum은 0.9로 동일하지만, weight decay는 0.005로 AlexNet에 비해 10배 늘렸다.
weight 초기화는 AlexNet과 동일하게 Gaussian 분포를 사용하였으나, 평균 0이지만, 분산은 0.1로 달랐다.
싱글모델로서는 D모델을 사용(7.2%)하지만, 성능을 높이고 싶다면 E모델을 앙상블로 사용한다(6.8%)
D모델(7.2%)은 싱글모델로서는 GoogleNet(7.9%)보다 좋다.
- 실용적인 면(메모리)에서 GoogleNet보다 D모델이 더 좋으면서, 연구가치도 높다. - input data의 전처리로서
이미지를 집어넣을 때, RGB값 각각의 평균을 빼는 작업을 통해, loss를 빨리 수렴하도록 만들었다.
512*512과 256*256를 --> 224*224로 여러개 crop한 뒤 학습시켰다.
그외 좌우반전 등을 이용하였다.
- ResNet(2015, 케이밍해, 중국 MS researcher -> 현재 페이스북)
- 2015년, error rate : 3.57%
- 152 Layers
- 일단 레이어수가 152개로 엄청나게 깊게 쌓았다.
- 인공지능의 목표인 인간의 한계(이미지넷 챌린지의 human performance error[논문용])인 5%를 넘어섰다.(3.57%)
이 이후로는, 이미지넷챌린지에서 classification문제는 나오지 않는다고 한다.... - VGGNet에서는 D모델(16)에서 E모델(19)로 Layer를 더 쌓았음에도 불구하고 성능이 늘어나지 않는 것에 대해,
케이밍 해는 밝혀낸 것이다.
이전까지는 Layer를 쌓음에 따라, overfitting으로서, train은 나아지지만<-> test데이터에서 성능이 안나왔다.
하지만 케이밍 해는 ResNet으로 20-> 56 Layer로 늘렸음에도 불구하고, train과 test데이터의 성능이 같이 안좋아졌다.
그 결과 Layer를 쌓는 것이 Overfitting의 문제는 아니라는 것을 먼저 밝혀냈다.
또, Layer를 쌓음에 따라서, 후반부의 Layer들이 training되지 않는 degradation problem을 발견했다.
그리고 이 degradation problem문제를 해결하기 위해서, Skip-Connection Layer라는 것을 도입하게 된다.
이러한 Skip-Connection Layer에는 Residual Block이라는 개념이 사용되었기 때문에 Deep Residual Network라 불린다.
Skip Layer는 아주 간단하다.
이전 VGGNet에서는 Conv Layer에 input x가 들어가서 H(x)가 나왔는데,
Residual Net에서는 x가 들어간 Conv Layer의 결과를 F(x)라 보고, input인 x를 더 해서 H(x) = F(x) + x로 하였다.
이 작업을 매 Conv Layer 2개 마다 이 작업을 해주는 것이다.
왜 이러한 것이 더 좋은 성능을 내는지 명확하게는 증명되지 않았지만,
x가 들어가서 새로운 H(x)를 내는 것보다, 원본x까지 포함되어, H(x)를 원본x의 변형된 버전으로서, 더 학습이 잘된다는 것이다. - VGGNet에서는 3*3 필터만 사용했지만, ResNet에서는 1*1 Conv Layer를 활용하여,
Featuremap의 차원을 축소하는 bottle neck개념도 사용되었다. - 또다른 특징으로
모든 레이어에 Batch Normalization을 적용하였다.
- Batch Norm은, weight가 업데이트과정에서 커저버려, output = 다음 Layer로 들어갈 input이 매우 커지는 것을 방지하기 위해,
output인 actavation값을 평균0, 표준편차 1로 만드는 standardization개념 + 상수 곱하고 + 상수 더하기
weight 초기화를 He initialization을 새롭게 적용하였다.(케이밍해가 만든 웨이트 초기화법)
SGD- Momentum 0.9는 VGG와 유사하지만, weight decay는 1e-5이다.
Dropout을 사용하지 않는 것이 VGG와 가장 큰 차이점이다. - 성능에 있어서, error rate는 싱글모델이 4.49% 앙상블 3.57%를 차지했다.
- Wide ResNet (2016년)
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
5. Convolutional Neural Network (이미지용 M.L.N.N.) - Convolution Filter / Max Pooling / keras 의 등장
지금까지 x1, x2, x3, .. 등의 feature데이터가 주어지고 + 정답인 y이라는 label데이터가 주어진 상황에서
답을 아는 상황이므로 Machine Learning 중 supervised learning에 해당하고,
그 가운데 위의 데이터를 Regression모델( Linear,Logistic, A.N.N.) 중 컴퓨터의 뉴럴네트워크인 A.N.N.알고리즘를 사용하여 푸는데
가장 효율적으로 문제를 해결(weight와 bias를 구하는 optimalization)하는 Gradient Descent을 통해 학습시켰다.
1. Regression문제 by Single-Layer N.N. (보스턴 집값예측)
2.3. Classification문제 by Single-Layer -> Multi-Layer ( MNIST -> MNIST 정확도향상)
이 Multi-Layer Neural Network가 바로 딥러닝의 prototype이라 할 수 있다. 보통은 3개 이상의 hidden layer가 들어간 것이 딥러닝이다.
이번 시간에는 Multi-Layer Neural Network 를 이미지전용으로 개선한 Convolutional Neural Network에 대해 학습해보자.
Multi-Layer Neural Network는 여러종류가 있으며, 그 중 하나가 Convolutional Neural Network라 생각하면 된다.
Convolutional N. N.
딥러닝을 가장 실용적으로 쓸 수 있는 알고리즘으로서, Multi-Layer Neural Network의 응용이다.
여태껏 A.N.N.을 python으로만 짜왔으나, 너무 복잡한 코드가 나오기 때문에, keras라는 툴을 사용하여 코드를 작성할 것이다.
Convolutional N.N.은 원리는 어렵지 않으나, 차원의 개념(4차원)이 어렵다.
4. 저번시간에 했던 Multi-Layer Neural Network는 Feed-forward N. N. or fully-connected N.N.이다.
MNIST dataset(28*28)은 흑백사진(0~255)으로, 픽셀단위(784)로 집어넣으면 ---> ouput은 0부터 9까지 10개가 나왔다.
M.L.N.N.의 이미지용 버전인 C.N.N.를 사용하면 아래와 같은 컬러사진을 binary classification으로 풀 수 있다.
어떤 칼라사진(28*28*3) (RGB, 3개가 각각 0~255)을 집어넣어서 ---> output 고양이 or 개인지 1개만 나오면 되는 binary classification을 풀 수있다.
얼굴사진도 인식 가능하다.
input Layer로 360*270pixel의 컬러사진(3)을 input으로 넣으면 output으로 특정사람인지/아닌지을 binary classification하는 모델이다.
여태껏 사용한 M.L.N.N.인 Fully-connected = feed-forward N.N.는 이미지를 분류하는데 있어서 나쁘진 않지만 비효율적인 면이 있다.
컬러 얼굴사진을 인식한다는 것은 RGB로 구성된 pixel이 있고,
해당pixel과 주변pixel을 출력함으로써--> 눈이구나 코이구나 입이구나를 먼저 알 수 있고,
눈, 코, 입의 구분을 조합함으로써 ---> 어떤 사람인지를 알 수 있게 된다.
이미지 데이터의 저장과 표현 중에서 반대로 locally-connected라는 것이 있다.
1) 특정 픽셀에 대해서 거리가 가까운 pixel은 연관성이 있어서 계산을 하고,
2) 거리가 먼 pixel은 연관성이 없는 것으로 보고서 계산하지 않는 방식이다..
fully-connected N.N. ( feed-forward) 방식의 문제점 살펴보기
만약, 위의 컬러얼굴사진을 Multi-Layer Neural Network의 input으로 집어넣었다고 가정해보자.
왼쪽위의 픽셀은 x1으로 들어가고, 오른쪽아래의 픽셀은 bias바로 위의 xn으로 들어갈것이다.
만약, fully-connect N.N.에서는 x1과 xn를 담당하는 w1과 wn사이의연관 관계를 계산해 줄것이다.
하지만 일반적인 이미지데이터에 있어서, weight는 필요가 없을 것이다. 그러므로 이미지를 fully-connected N.N.에 넣어서 계산하는 것은 매우 비효율적이 된다.
한편, 이미지라는 것은 해당 object의 위치만 바꾸면, 똑같은 pixel(feature)임에도 다른 위치의 input으로 위치하게 된다.
만약, fully-connect N.N.는 feature의 위치에 민감하여 다른 입으로 인식할 것이다.
아래의 입의 첫pixel이 fully-connected N.N.의 위쪽으로 올라가서 위쪽의 feature로 인식될 것이다.
즉, input의 위치를 중요하게 여겨 weight로 연산된다.
하지만, 사람이 사진을 인식하는데 있어서, 입의 위치는 중요하지 않다.
즉, 똑같은 pixel은 다른 위치에 있더라도 똑같은 feature로 input되어야하는데,
fully-connected은 위치가 바뀐 동일 feature(pixel)에 대해서 hidden-Layer에서 동일한 feature을 중복해서 뽑아내게 된다.
요약하자면,
1)지금까지의 Multi-Layer Neural Network(fully-connected N.N.)는 이미지의 모든 픽셀의 연관관계를 한번에 모두 연산했다.
- > 이미지용 M.L.N.N.인 Convolutional N.N.는 검사하고 있는 특정픽셀이 선택된 시점에서, 주변픽셀과의 연관관계만 연산한다.
2) full-connected는 input으로 들어가는 pixel의 위치에 대한 weight가 중요하게 계산되어 동일 pixel이라도 다른것으로 인식되어 똑같은 feature를 extracor되었다.
- > C.N.N.은 input의 위치가 중요한게 아니라 입(object)을 뽑아내는 weight가 이미지를 돌아다니는 shared weight가 모든 이미지의 pixel을 돌아다니면서 해당 입(obejct)를 판별한다.
이러한 2가지 fully-connected의 문제점을 극복한 것이 바로 Convolutional N.N.이다. C.N.N.은 2가지 특징외에
1.
한번에 모두 검사하는 fully-connected는 가로 x 세로의 개념이 없었다. -> MNIST dataset처럼 다 펼쳐서 한번에 계산했다.
그러나 C.N.N.부터는 가로 x 세로의 개념이 있다.
2.
C.N.N.에는 Convolutional Filter가 있는 것이 핵심이다. 이 Convolutional Filter도 가로x세로의 개념이 있고, 돌아다니면서 연산한다.
32by32 이미지에다가 5by5의 컨볼루셔널 필터가 있다고 가정해보자.
이 필터는 좌상단에서부터 시작한다. 이러한 필터는 5by5만큼의 주변픽셀들만 연산하게 된다.
이미지의 좌상단 5by5 pixel과 필터 5by5가 서로 연산한다.
이미지의 5,5픽셀은 input * 필터의 5,5픽셀은 shared weight의 개념으로서 dot product하게 되면 output의 좌상단 1pixel이 된다.
연산의 순서는 좌상단에서 -> 오른쪽으로 1pixel씩 이동하며, 좌측으로 내려가 -> 오른쪽으로 진행된다.
이러한 방식을 sliding window라 한다.
참고) 인풋 이미지의 가로세로 32 - ( 필터가로세로5 -1) = output의 가로세로 가 된다.
이러한 Convolutional Filter는 이미지가 locally-conntected한 이미지데이터라는 것을 가정해야 나타나는 개념이다.
그래서 Filter는 현재위치의 1pixel과 그 1) 가로세로의 크기만큼의 주변pixel의 연관관계를 계산하게 되는 것이다.
2)인풋의 위치와 관계없이, 자기가 돌아다니는 shared weight로서 sliding window방식으로 돌아다니면서 dot product연산하여, 똑같은 feature라면 위치와 상관없이 해당feature를 잘 뽑아낼 수있게 된다.
정리하자면
C.N.N.은 가로*세로의 개념을 가지면서, Convolutional Filter(shared weight)가 sliding windwo방식으로 돌아다니면서 dot product한다.
나머지의 과정은 M.L.N.N.과 마찬가지로
#forward propagation을 통해 h(x) - y_predict -> L(y,h(x))까지 나오고
#back propagation을 통해 편미분하여 filter의 weight와 bias의 변화량을 알 수 있게 되고
Graident Descent로 반복해서 학습시킨다면, 최적의 w와 b가 나와서 이미지의 특성을 뽑아 줄 것이다.
C.N.N.의 Convolutional Filter가 효과가 있는지 판단해보자.
M.L.N.N.에 의한 딥러닝의 hidden Layer는 input에서 feature를 스스로 뽑아낸다고 했다.
즉, C.N.N.도 효과가 있는지 없는지에 대해서 판단하라면 hidden-Layer처럼 Convolution Filter가 스스로 feature를 뽑아내는지 확인하면 된다.
누군가가 C.N.N.의 각 Layer를 시각화 한 것이다.
- C.N.N.의 Layer는 앞쪽일수록 저차원의 linear한 feature를 뽑아내고, 뒤로 갈 수록 고차원의 feature를 뽑아낸다.
- Layer1은 선형을, Layer2는 타원모양으로 점점 feature를 뽑아내는 것을 알 수 있다.
-Layer3에서는 벌집모양의 feature를 뽑아낸다. 마지막 Layer에서는 자동차class에서 자동차의 특징인 본넷과 타이어를 뽑아내는 것을 알 수 있다.
결과적으로 C.N.N.의 Filter가 스스로 feature를 잘 뽑아내는 것을 알 수 있다.
그리고 그 방식은 M.L.N.N.보다 더 효율적이었다.
개별적인 6개의 Convolutional Filter 의 묶음 : Convolutional Layer
앞에서 본 Convolutional Filter는 2,2 혹은 5,5으로 weight가 작았다.
관례적으로 하나의 Filter당 하나의 feature를 뽑아낸다 고 얘기한다. 그러므로 여러개의 feature를 뽑아내기 위해서는 여러개의 Filter를 써야한다.
이 여러개의 Convolution Filter를 묶어놓은 것을 Convolution Layer라고 한다.
가로세로5 인 C. filter 6개를 묶어놓은 것을 Convolutional Layer라고 하며, Filter가 6개이므로 6개의 feature를 뽑아낸다.
기본적으로 weight처럼 6개의 Convolutional Filter는 서로 다른 랜덤 초기화 필터이다.
Convolutional filter는 sliding window방식으로 하나의 feature를 뽑아내는데,
하나로는 부족하니까 6개를 묶어서 쓴다. 그것을 Convolutional Layer라고 하는 것이다.
여기서 가장 많이 헤깔리는 것이 filter_size에 대한 것이다.
input은 컬러이미지로서, 가로32세로32 RGB3개이다. 여기에 데이터의 갯수가 더 붙을 것이다.
- 여기서 RGB 3개를 input Filter size라고 한다. 인풋으로 넣는 데이터의 필터(RGB)의 갯수가 3개인 것이다.
Convolutional Filter는 shared weight로서, 가로5,세로5를 가지며, filter size도 붙는다.
- Convolutional Filter의 filter size는 그것은 input filter size(데이터필터갯수ex>RGB)와 하다.
인풋이미지와 연산을 할 때, 흑백이면 흑백 (1), 칼라면 칼라(RGB, 3)이 같은 상태로 연산해야되기 때문이다.
하지만 그 값은 output으로 나갈 때, 1이 되어버린다.
즉, input_filter_size(3) 과 convolution filter_size(3)는 같아야하며 연산결과는 1로 고정되어, 무조건 1이다.
하지만, Filter가 모여있는 Layer안에서는 총 필터 갯수가 6개이므로 output_filtersize는 6이 될 것이다.
Output의 연산 결과는 ouput size가 input size와 같거나(나중 나올 개념) 작아진다(앞에서 나온 개념) 32*32 -> 28*28
- output_Filter_size는 Filter 6개가 모인, Convolutional Layer의 전체 연산결과로서, 1+1+1+1+1+1 = 6이다.
요약하자면)
Filter_size : intput(3) = convolutional Filter(3) ---> 연산 후 (1) ---> 6개가 모인 Convolutional Layer (6) = output (6)
이제 Filter_size의 개념이 제대로 이해가 되었다면, input에 넣는 데이터 4가지를 살펴보자. (여기서는 데이터의 갯수 제외하고 3가지만)
1. input으로 (세로, 가로, input_filter_size) ( 32, 32, 3 )에서 맨마지막input_filter_size는 컬러라면 3으로 고정
2. Convolution Filter(weight)는 처음인자가 늘어나서 (output_filter_size, input_filter_size, 세로, 가로) ( 6, 3, 5, 5)인데,
output_filter_size는 C.N.N.이라면 Convolutional Layer 속 filter갯수만큼 6으로 고정이다.
3. output도 input과 비슷한 형태의 (세로, 가로, output_filter_size)인데, 맨 마지막 output_filter_size는 1짜리 6개로 6으로 고정
이렇게 input과 Convolution Filter의 데이터를 정확히 맞춰주어야 -> C.N.N.가 돌아가서 연산되고 -> output이 나오게 된다.
여기서 헤깔리는 개념은
각 Convolutional Filter는 6개가 각각 연산해서 각각 6개의 output을 만들어내는 것이다. 그리고 그 output은 새로운 feature로서 6개가 쌓이는데 output feature라고 부른다.
input은 비록 이미지를 넣어줬지만(input feature), output feature는 더이상 이미지가 아니게 된다. 그러므로 resizing 코드들이 먹지않는다.
이 때, Convolution Layer의 갯수는 임의로 지정할 수 있다. 나중에 학습할 것이다.
여러개의 Convolutional Layer로 구성할 수 도 있다는 것만 알아두자. 각각의 input feature - Convolution Filter 6개의 Convolution Layer - 6개 각각의 연산결과의 6개 output feature 정도의 구성이다.
여기서 이해해할 개념은 input_fillter_size와 output_filter_size를 이해하는 것이 먼저이다.
- input_filter_size와 convolutional filter의 filter_size는 똑같이 가야한다.
- output_filter_size와 convolutional Layer의 filter개수는 똑같아야한다.
Max Pooling
예전에는 이 Max pooling을 많이 사용하면서 권장하였지만, 요즘의 실용적인 접근에 있어서 많이 안쓰려고 하는 추세이다.
연구쪽에서는 특히나 많이 빼는 추세이다.
Max Pooling은 데이터의 사이즈를 강제로 줄이는 개념이다. 구체적으로 Max한 큰값만 챙기고 작은 값은 버리는 개념이다.
마치 Convolution Filter(shared weight)처럼, Pooling이라는 것이 sliding window방식으로 우측으로 가면서,
이 때, 1 pixel씩 우측으로 가는 것이 아니라, 자기의 size만큼 우측으로 가거나/하단으로 내려간다. 기본적인 Pooling Filter의 크기는 2by2이므로 2칸씩 가게 된다.
그러면서 Pooling의 사이즈안에 있는 값 중 가장 큰값만 챙기고 다른 작은값들은 버린다.
( Filter는 우측으로 1pixel씩 가면서 dot product로 연산하였다면, Pooling은 자기 사이즈씩 가면서 큰 값만 취한다.)
예를 들어, Input feature가 (4,4)이고, Pooling이 (2,2)--> output feature가 (2,2)라고 가정해보자.
여기서 Max Pooling을 하면서 왜 꼭 값을 버려야하냐는 의문이 제기 될 수 있다.
고양이 사진을 예를 들어보자.
고양이의 사진 중에서 고양이의 특징을 나타내는 픽셀은 그렇게 많지 않다. 연산을 효율적으로 하기 위한 방법 중 하나가 이 사진이 고양인지 아닌지 나타내는 중요한 pixel부터 먼저 뽑아놓고 연산하는 방식이 있을 것이다.
Max Pooling의 위치는 가능한 Convolution Layer 다음에 집어넣어서 ,
CONVolutional L. -> Max Pooling -> CONVolutional L. -> Max Pooling -> CONVolutional L. -> Max Pooling을 반복하여 쌓는다.
아니면 CONVolutional L. -> CONVolutional L. -> Max Pooling ->CONVolutional L. -> CONVolutional L. -> Max Pooling 식으로 쌓는다.
이렇게 되면, Convolutional Layer의 연산을 거친 output feature 중에서 값이 큰 것만을 남겨서 다음 Convolutional Layer에 들어가게 된다.
앞에 위치한 Convolutional Layer에서는 중요한 고양이 feature가 발견되면 값을 크게 주게 될 것이다.
즉, 필요없는 feature를 버려서, 남은 메모리는 다음 Conv Layer를 쌓는데 쓰는, 연산을 효율적으로 만든다는 뜻이다.
여기서, Activation(앞에서 배운 sigmoid처럼, output feature의 값이 0~1사이로 나타내는, a(x), h(x)전에 z(x)에서 씌우는 것)까지 생각해보면,
Conv L. -> ActV -> Conv L. -> ActV -> MaxPooling 또는
Conv L. -> ActV -> MaxPooling -> Conv L. -> ActV -> MaxPooling 의 방식으로 반복되어서 층을 쌓는다.
마지막으로 맨 마지막 층에는 한번에 모든 픽셀을 다 검사하는 fully-connected Neural Network(기본적인 Multi-Layer Neural Network)를 넣는다.
요약하자면
Convolutional Neural Network는,
여태껏 배운 Multi-Layer Neural Network(fully-connected) 앞에 Convolutional Layer(locally-connected)가 여러개 들어간다.
실습 - keras
빅3 모듈 : tensorfow / keras / pytorch가 있는데, 요즘은 pytorch가 잘나가고 있다.
- keras의 단점은 조금 느리나, 엄청 심플하다는 것이 특징이다. 나중에 고성능으로 딥러닝을 짜야한다면, tensorflow나 python를 배우면 된다.
keras로 MNIST를 튜닝해보자.
keras로 가장 default한 딥러닝 모델( Single-Layer ) 구성해보기
(Single-Layer나 Multi-Layer는 fully connected N.N.로서, (세로,가로)의 개념이 없기 때문에 pixel을 다 펼친다 (세로*가로))
1) keras/numpy/pandas모듈 가져오기
2) keras.datasets모듈에서 mnist데이터셋 가져오기 -> shape확인하기
3) 가져온y_train의 10개만 확인해보고 -> X_train(feature)를 10개도 시각화해서 label과 매칭해보기
4) Single-Layer나 Multi-Layer는 fully-connected로서 나눠진 세로,가로 픽셀을 reshape로 펼치기
5) keras.utils모듈 속 to_categorical로 쉽게 label들(y_train, y_test) 원핫인코딩 하기-->y_train_hot, y_test_hot
6) Single-Layer그림을 생각해보고, keras로 Single-Layer 구현하기
- 딥러닝 model구현을 위한 default model인 Sequential()받아오기
mode.add()를 통해 dense(weight층)을 집어넣어준다.
- keras의 Dense - fully-connected N.N.의 weight --> model.add를 통해 weight에 해당하는 Dense( , , )인자로 3가지를 지정해줘야한다.
(1)먼저 output_size인 10을 units인자에준다. (units=10,
(2) input_size인 784는 input_shape 인자로 준다.(input_shape=(784,)
(3) 마지막으로 weight인 Dense에다가 actvation도 함께 지정해준다.
- keras의 compile - add해준 모델을 최종 생성하는 역활 -> compile(, ,)에서는 2가지 인자를 지정해줘야한다.
(1) 편미분시켜서 최종적인 w와 b를 찾아가는 기법인 optimizer를 지정
(여태껏 배운 가장 기본적인 gradient descent인 sgd - stochastic gradient descent 를 배웠다)
(2) loss함수 지정 -> multi-classification문제이므로, classification용 loss함수인 'categorical_crossentropy'를 지정해준다.
- keras의 fit - 생성한 모델의 학습을 시작 -> fit( , , )의 필수 3가지 인자로는
(1) feature데이터(input feature, X_train) ,
(2) 핫버전의 label데이터 ( y_train_hot )
(3) epoch인자로 학습 수 지정( epoch = 20 )
(4) 선택적으로 검증데이터가 있다면 검증데이터의 feature데이터 + hot버전의 label데이터 지정 ( validation_data = ( X_train, y_train_hot))
- 정확도 비교가 아니라 gradient 태워서 학습하는 중이므로 hot버전의 label데이터로 학습시킨다.
여기까지가 keras로 single-Layer를 구성하는 default를 구성이다.
default + accuracy 출력(compile시) + 검증데이터 이용(fit시)
여기에 complie로 모델을 생성할 때, 학습과정 중에 해당항목을 출력해주는 metrics(측정항목)을 통해 accuracy를 지정출력해보자.
fit.으로 학습시킬 때, 검증데이터를 집어넣어주는 validation_data를 통해 test set을 검증데이터로 지정해보자.
- epoch을 돌 때마다, train 과 validation set의 loss / accuracy가 같이 표시된다.
- 앞으로도 train시킬 때는, train data를 / validate할 때는 test data를 집어넣자.!
keras.optimizers모듈로 특정 Optimizer 사용하면서 learning_rate추가해주기
- from keras.optimizers import SGD 로 사용할 특정 optimizer를 추가해준다.
- optimizer변수로 따로 받음과 동시에 learning_rate를 지정해 줄 수 있다.
optimizer = SGD(lr = 0.00001)
아직까지는 loss값이나 accuracy가 너무 좋지않다.( 1/10씩 줄거나 마지막자리수를 올리는 방법을 써봐도 별로 개선되지 않았음)
learning_rate를 조절해도 개선되지 않을 때는, weight를 조절해주는 방법을 쓸 수 있다.
앞에서 python으로 딥러닝모델을 만들 때는, -1 ~ 1까지 weight의 사이즈를 임의로 지정해서 랜덤초기화 하였다.
다음시간에는 구체적인 weight 범위조절 및 초기화 방식을 알아볼 것이다.
지금은 가볍게 weight초기화를 조절하여 loss를 줄이고 accuracy를 올리는 것을 구현해보자.
keras.initializers 모듈의 RandomUniform를 통해 weight초기화 조절해보기
- from keras.initializers import RandomUniform 를 통해 주사위를 던지는 것과 동일하게 1,2,3,4,5,6을 균등하게 랜덤으로 가져오는 모듈사용
- compile로 학습모델 생성시,weight에 해당하는 Dense의 인자로 kernel_initializer = RandomUniform(minval = 0.0, maxval = 0.001)를 추가해주자. 범위는 임의로 최소값(minval=) 0.0부터 최대값(maxval=)0.001 까지의 weight를 가지도록 지정해주자.
loss가 급격히 줄면서 accuracy가 결국에는 87%까지 올라갔다.!!!
Keras로 MNIST(multi-classification)문제를 풀기 위한 Multi-Layer Neural Network 구성해보기
위 사진과 같이 Dense가 2개가 들어간다.
1. 먼저 그림속 weight의 input / output을 생각하면서 ---> Dense를 작성한다.
- 여기서 재밌는 것은 2번째 Dense(Layer)의 input(intput_shape)부터는 이전의 Dense이 output(units)와 동일하기 때문에
input_shape를 생략한다.
2. keras라도, Multi-Layer N.N.부터는 오래걸리니 epoch수를 1/2로 줄였다.
3. 똑같이 fit해준다.
Keras로 MNIST(multi-classification)문제를 풀기 위한 C.N.N. 구성해보기
single-Layer, Multi-Layer N.N.와 다르게 C.N.N.부터는 세로 * 가로의 개념이 있게되어, shape계산을 잘해야한다.
1. feature 데이터(X_train, X_test)를 다시 reshape해준다.
input(input feature, feature데이터)이 기본적으로 4가지가 들어가야한다. ( 데이터, 세로, 가로, 필터사이즈 )
- MNIST는 기본적으로 흑백이므로 input_filter_size가 1이다
2. keras로 C.N.N. 모델을 만들어보자.
- 멀티레이어 N.N.의 코드를 복붙한다음,
- keras.layers 모듈에서 가져왔던 Dense(weight) 이외에 Conv2D, MaxPooling2D, Flatten 모듈도 가져온다.
컨브투D는 컨볼루셔널 레이어 / 맥스풀링투D는 맥스풀링 레이어 /
플래튼은 C.N.N. 마지막 층에 들어가는 Single or Multi-Layer로 변환하기 위해 세로*가로개념을 하나로 펼쳐준다. 펼쳐준다.
즉, (세로,가로,필터사이즈) 의 개념이 있는 Convolutional Layer에서--> 세로가로개념이 없는 fully-connected인 Single-/Multi-Layer에 넣어주기 위해 펼쳐준다
- 이제 Sequential()에서 가져온 model변수에 .add( Dense가 아닌 Conv2D를 추가한다.
3. Conv2D(Convolutional Layer)에서는 먼저
(1) filters 인자에 filter의 개수를 정할 수 있다. 기본적으로 filter는 6개를 쓰고 그결과 output feature의 필터사이즈도 6이었다.
(2) kernel_size는 filter의 (세로,가로) size이다. 위에서 본대로 (5,5) 필터를 사용하자.
(3) 다음으로 activation인자로 activation function을 지정해준다. ( 따로 .add해도 된다 Conv->Activ->Conv->Activ-> Pool )
(4) intput_shape로 input_size(세로,가로)를 정해준다.
* Single-/Multi-Layer에서는 fully-connected된 weight개념으로 Dense, input_shape가 세로가로 개념이 없어서 (784,)
* Convolutional Layer에서는 locally-connecte된 이미지를 특정한 크기를( kernerl_size(5,5)) Filters 6개가 연산하는 Conv2D, input세로가로 개념이 생기고 input_filter_size(색)의 개념도 생겨서 input_shape(28, 28,1)
--> 내부적으로 Convolutional Layer의 size는 (6, 1, 32, 32) - (output filter_size = filters, input_filter_size, input_size(height), (width))
4. Conv2D (-> Actv) -> Maxpooling2D 차례이다.
(1) pool_size로 Pooling의 사이즈를 지정해준다. 임의로 (2,2)를 사용해보자.
(2) strides로 pooling이 좌상단->우하단으로 점프를 뛰는 것을 지정해준다. 자기 size와 똑같이 (2,2)를 주는 것이 특이하다.한칸 뛰고 싶다면 (1,1)
5. 이제 Conv2D (->Actv ) -> Maxpooling2D를 반복해준다.
- 너무 똑같이 하지말고, Conv2D ( Convolutional Layer의 필터갯수를 12개로 지정해줬다)
- input_shape는 알아서 계산되니, 삭제하자.
6. Conv2D (->Actv ) -> Maxpooling2D를 반복이 끝난 마지막 단계에서는 Single-/Mult-Layer가 들어가는데, Flatten()모듈로 (세로,가로,input_filter_size) 개념을 하나로 펼쳐준다. 즉, Convolution 연산이 끝나면, Flatten()한 다음, fully-connected에 넣어준다는 개념!
7. Multi-Layer N.N.를 작성할 때 쓴 Dense코드를 가져와서 mode.add(Flatten())다음에, Multi-Layer N.N.를 구성해준다.
- 노드는 임의로 128개로 주자. output feature이므로 units 인자에 들어갈 것임. 뒤쪽Layer이므로 input_shape는 필요없다.
8. 마지막으로 X_test로 모델검증을 하려면 model.predict( X_test) 를 통해 예측값(hot버전)을 array를 반환받는다.
실제데이터와 비교를 통해서 정확도를 평가하려면 롤백해야한다.
- keras의 모델생성(compile)/학습(fit)/검증(predict)은 모두 hot버전인 상태이다. 정확도 평가를 위해서는 argmax(axis=1)로 롤백 해야한다.
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
4. Multi-Layer Neural Network for XOR problem - Back propagation의 등장 / MNIST 성능올리기
지금까지 배운 것들의 한계
지금까지는
1. Regression문제해결을 위한 Regression버전의 Single-Layer Neural Network
- input을 넣으면 z(x)가 바로 w1x1 +b형태로 나옴
2. Binary classification 문제해결을 위한 Binary classification 버전의 Single-Layer Neural Network
- classification을 위해서는 h(x)가 0~1의 확률값으로 나와야 0.5를 기준으로 squarshing할 수 있는데,
- h(x)를 변환시키기 위한 sqaursh func인 sigmoid를 z(x) = w1x1+b에 입힌 sigmoid(z(x))가 h(x)
3. Multi-class classification 문제해결을 위한 Multi-class classification 버전의 Single-Layer Neural Network
- binary classifcation버전에서 h(x)가 여러개가 나오는 경우이다.
- 각각의 output(h(x)) 중 어느 것을 선택할 지에 대한 각각의 확률이 나오도록
- y(label)은 0,1,2순으로 미리 구성이 되어있어야하며 --> one-hot-encoding시킨 y_hot을 구한다.
- y_hot을 정답을 바탕으로 학습하여 도출된 y_predict_hot 버전으로 w를 업데이트한다.
- 정확도 비교를 위해서 y(label)와 y_predic(h(x))는 다시 0,1,2순으로 롤백하도록 argmax(axis=1)를 이용한다.
을 학습하였다.
그 가운데, binary classification버전의 Single-Layer Neural Network를 사용하여,
- 정답y는 이미 0 or 1의 값을 가지고 있어서, ( y> 0 ).astyle('int')를 이용해서 0과 1으로 squarshing하였다.
- 예측값y_predict(h(x))는 Regression버전(무한대의 예측값)--> sigmoid로 0~1값을 가지게 만들고 --> ( y>=0.5).astype('int')를 이용해서 0 or 1로 squarshing 하여 Classification버전으로 바꾸었다.
feature인 x1과 x2의 데이터에 따른 y(label)을 찍어보면, 0일 때는, 보라색 / 1일 때는 노란색으로 그림이 나타났다.
그 기준이 되는 것이 ( y_predict >=0.5 ).astype('int')를 이용하여 sigmoid(h(x))의 결과값들을 0과 1로 잘라낸 0.5이다.
마치 하나의 선이 있는 것 같아보인다. 그 선의 아래부분에 있는 것들은 y값이 0, 위에 있는 것들이 y값이 1이 나온다.
이러한 기준이 되는 선을 Decision Boundary라고 한다.
이 Decision Boundary의 공식을 유도하고, 그것을 이용해 코드로 시각화 해보자.
먼저, h(x)의 결과가 0or1로 squarshing해주는 기준인, h(x) = 0.5인 지점을 찾아야한다.
Decision Boundary는 y_predict = h(x) = 1/2 인 지점인들인데, sigmoid(z(x)) = 1 / 1 + e ^-(z(x)) = 1/2 지점을 찾아야한다.
곧, z(x) = 1이 되는 지점들이다. 즉, w1x1 + w2x2 + b = 1인 지점들이,
classification 문제에서 예측값을 0or1로 판단하는 지점인, Decision Boundary이다.
x1이 주어진다고 가정하면,(x축, 코드상 xx, linspace로 지정해줄 것임)
x2(y축, 코드상 yy)가 - (w1x2 +b)/ w2인 지점들이다.
코드로 표현해주면 아래와 같다.
요약)
아~, 그럼 h(x)를 0 or 1로 squarshing 해주는 기준인 1/2 = h(x)지점이 Decision Boundary라고 하고,
Decision Boundary를 그려서 정확히 보라색점(h(x)=0)과 노란색점(h(x)=1)이 나누어지면,
binary classification버전의 Single-Layer Neural Network로 풀어지는 문제구나 생각할 수 있다.
아래의 데이터셋이 S.L.N.N.로 풀 수 있는지 없는지 확인해보자.
1. AND dataset / OR dataset --> Single-Layer Neural Network로 풀자
- 왜냐하면, Decision Boundary가 그려져서 정확히 classification할 수 있으니까.
2. XOR dataset ===> Multi-Layer Neural Network 로 풀자.
- 왜냐하면, Decision Boundary가 그려지지 않아서 Single-Layer N.N.로는 classification되지 않으니까.
- feature만 변형하는 방법 /
어떤 데이터가 주어졌을 때
Single-Layer Neural Network 로 풀 수 있는가 없는가? 를 판단할 때는,
시각화 하여 그래프 상으로 Decision Boundary로 그릴 수 있는가 없는가로
판단하면 된다.
- AND DATASET 와 OR DATASET을 Single-Layer N.N.로 풀 수 있는지 없는지 알아보자.
( 그래프상에서 점(y_predict)가 1이면 O, 0이면 X로 표시하였다) - XOR DATASET : x1과 x2가 동일하면 0, 다르면 1 --> Decision Boundary를 그리지 못한다. Single-Layer N.N.로 못푸는 문제
Single-Layer N.N.로 풀지못하는 데이터를 풀기 위한 방법
1. dataset 자체를 변형한다.
싱글 레이어 뉴럴 네트워크로 풀지못하는 XOR데이터셋을 변형시켜 풀 수 있도록 해보자.
y는 XOR 데이터 그대로 가져온다. (0 , 1, 1, 0) x1과 x2를 바꾸는데, AND( x1 !, x2 ) | AND( x1, x2 !) | y 를 그려보자.
이것을 시각화 해보자.
요약하자면)
Single-Layer N.N.로 풀지못하는 문제를 만났을 때,
y(label)은 그대로두고, x(feature)만 어떻게 바꾸면 된다.
이렇게 Single-Layer로 못푸는 문제를 feature를 모조의 수단으로 바꾸어서 Decision Boundary를 그릴 수 있게 바꾸어서 풀 수 있다.
코드를 통해 AND/OR데이터는 w와 b를 잘 학습하여 정확한 accuracy가 나오는지
XOR데이터는 S.L.N.N로 w와 b를 제대로 학습하지못하여 낮은 accuracy가 나오는지 확인해보자.
feature를 S.L.N.N로 풀수 있게 새로운 feature로 변형하는 과정은.. 기존 Single-Layer N.N. 앞에 하나의 layer가 더 있는 형태이다.
즉, [] [] 의 S.L.N.N.를 ---> [] [] [] 가운데 hiden layer를 넣은 형태로서, 맨 마지막 Layer를 S.L.N.N로서 풀면 된다. [] [] []
이후 이러한 새로운 방식의 아키텍쳐를 배울 것이다.
2. feature를 polynomial 방식으로 늘려준다
y = w1x1+w2x2+b의 w와 b를 학습하는데 있어서, x1과 x2가 XOR데이터일 경우 S.L.N.N [] [] 형태로는 잘 풀지 못하였다.
Polynomial 이라는 것은 dataset의 feature인 x1, x2를 서로 곱하거나, 제곱, 세제곱하여 차원을 늘려주는 방식이다.
이론적으로는, 다양한 x, x^2, x^3 ... 중에 decision boundary를 그릴 수 있는 x(feature)가 걸리면 정확하게 예측한다는 내용이다.
코드상으로는 x1, x2, x1^2 = x3, x1*x2=x4, x2^2=x5 까지 만든 뒤, 새로운 polynomial dataset를 S.L.N.N형태로 Gradient Descent를 태워보자.
3. Multi-Layer Neural Network
Decision Boundary를 그릴 수 없는 것으로 S.L.N.N.로 풀지못하는 문제로 판단한 XOR dataset은
- Dataset을 label은 유지한 체, feature를 모종의 방법(flipped & and)으로 뒤집어 변환하기
- Dataset을 label은 유지한 체, feature를 Polynomial 방식으로 늘여주기
를 통해 해결할 수 있었다. 하지만, 각각의 단점이 있었다. 이러한 문제를 해결하는 방법이 Multi-Layer Neural Network이다.
특히 범용적이었던 Polymonial dataset은 feature가 늘어남에 따라, 메모리를 왕창 잡아먹는 단점이 있었다.
범용적이면서 좀 더 효율적으로 XOR problem을 푸는 방식이 바로 Multi-Layer Neural Network이다.
Multi-Layer Neural Network
Single-Layer Neural Network(perceptron)로 풀지 못하는(Decision Boundary) 그릴 수없는) Data에 대한 해결책으로 나온
Multi-Layer Neural Network(Multi Layer Perceptron)에 대해서 알아보자.
Multi-Layer Neural Network는 Multi-Layer Perceptron(M.L.P)는 완전히 동일한 용어다.
Single-Layer N.N.와의 가장 큰 차이점은 hidden Layer가 들어가는것이다. 이 히든 레이어가 M.L.N.N, 딥러닝의 핵심이다.
처음 들어가는 feature + bias를 input Layer, 마지막을 output Layer이라고 하고
각 Layer를 구성하는 것을 neuron이라한다.
hidden Layer의 갯수는 우리가 직접 수정가능하다.
맨 마지막 hidden Layer - output Layer는 input---> weight---> output이 나오는 Single-Layer Neural Network이다.
input Layer - 첫번째 hidden Layer는 feature extractor라고 한다. M.L.N.N.의 핵심이다.
- 인풋을 집어넣으면, 알고리즘이 잘 학습됬다는 가정하에, feature를 집어넣으면 그것을 바탕으로
앞부분의 hidden Layer들로 구성된 feature Extractor가 맨 마지막의 Single-Layer N.N.가 classification할 수 있도록 해주는 새로운 feature를 뽑아내주는 역할을 한다.
즉, 다시 말하면 M.L.N.N.는 S.L.N.N.의 앞부분에 hidden Layer가 임의의개수만큼 들어가서
각 hidden Layer들은 새로운 feature들을 층 수 만큼 계속 뽑아내서, 최종적으로는 마지막의 Single-Layer Neural Network가 classification할 수 있는 새로운 feature를 전달해주어서 classification을 끝낼 수 있다.
범용적이었던Polynomial 과는 다르게, hidden Layer와 neuron의 갯수를 자유자제로 조절해줄 수 있기 때문에, 메모리 효율적이다.
hidden Layer가 1개만 있어도 Mulit-Layer Neural Network이며,
hidden Layer가 3개이상을 Deep Learning 이라 한다.
이제 XOR dataset 전용으로 Multi-Layer Neural Network를 그려보자.
위의 내용처럼, feature extracor로 인한 w가 더 늘어난 상황이다.
Gradient Descent를 태우기 위해서, 각각의 w1, w2에 대한 1개의 cost function의 변화량을 알아야, w의 업데이트가 가능해진다.
이러한 문제 - 2개의 w에 대한 1개의 cost functin 편미분(=결국 loss function 편미분)을 해결하기 위한 방법이 하는 back propagation이다.
편미분시 chain rule을 활용하여, 여러개로 쪼개어서 하나하나 구한 뒤, 곱하는 것. 그것이 바로 back progapation이다.
Back propagation( 역전파 알고리즘) for M.L.N.N.의 w,b업데이트량을 구하기 위해 사용하는 기법
back propagation의 공식을 유도해보자. 이 때, cost function과 loss function은 같은 개념으로 본다.
먼저 foward propagation을 알아보자.
input(X)을 넣은 다음, 마지막 h(x) ( y_predict)까지 나오는 과정을 forward propagation이라 한다.
forward propagation을 통해 예측값인 h(x)가 구해진다면,
L(y,h(x))를 정의할 수 있게 되고, loss function을 편미분하여 w2를 먼저 구할 수 있게 된다.
w2의 편미분 구해진 것을 이용하면 w1 편미분도 쉽게 구할 수 있게 되는데, w2, w1의 변화량이 구해졌다면
gradient를 태워 w1, w2를 업데이트 할 수 있게 된다. 이러한 과정을 Backpropagation이라 한다.
train은 forward -> back를 한 싸이클로 계속 반복하여 train시킨다.
요약하자면
Input(X, feature) ------> z1-(sigmoid for classification)->a1-------> z2-(sigmoid)->a2 = h(x) : forward propagation
h(x)---> L(y,h(x)) ------> w2 변화량 ------> w1변화량 ----(gradient descent)---> w1, w2, b1, b2 업데이트 : back propagation
my) loss function 은 a2인 h(x)를 가지고 있는 맨 마지막 Singlel-Layer쪽에서만 나오는 용어이다.
w1, w2를 편미분한 w1, w2 변화량을 구하는 것이 중요하다. 공식을 유도하여 코드를 도출해보자.
먼저 single-layer쪽이라서, h(x)-> L(y,h(x)) w2를 편미분하여 w2의 변화량을 구하는데, 편미분 할 때, chain rule을 활용하여 쉽게 계산한다.
그 계산과정에서 어떤 값들을 캐슁해놓으면, w1 편미분도 쉽게 구할 수 있게 된다.
w2에 대한 Loss function의 변화량 과 w1에 대한 것이다.
먼저 w2의 변화량을 chain rule을 적용하여 a2, z2를 활용하여 3단계로 나눈뒤, 각각 구하고, 곱해보자.
결과적으로, w2변화량 (w2업데이트 량)은 (a2 - y)a1으로 구해졌다.
w1을 구하는데, 총 5개로 쪼개어졌으며, 그 중 앞부분 2개의 미분은 w2변화량 시 구한 3개의 편미분 중 2개(1,2)가 겹친다..
그리고 마지막 2개는 w2변화량 시 구한 3개의 편미분 과 이름만 a2->a1으로 다르니, 구한것에 이름고, 참고한다.
w1, w2에 대한 cost function(loss function)변화량을 알아보았다. 마찬가지로 b2, b1의 변화량도 구해야하지만 생략한다.
결과적으로 여기서의 M.L.N.N.에서 Gradient Descent를 태우기위한 w2,w1,b2,b1의 업데이트 량은 아래와 같다.
결론적으로 코드상 캐슁효과를 내기 위해,
- a2-y 는 전부 겹친다
- a2-y * w2 * a1 * (1-a1) 은 w1과 b1의 변화량 구할때 겹친다.
두 수식을 Gradient의 for문안에서 backpropagation 부분에 캐슁해놓을 것이다.
참고)
Single-Layer N.N. for Multi-classification (iris dataset문제)에서도 w는 matrix였다.
Multi-Layer N.N.의 w1 과 w2도 기본적으로 matrix( input(feature)수 , output(a1(x) or a2(x) = h(x) 수 )
bias도 마찬가지이다. 대신 input은 1개로 고정된다.
이제 코드상으로 Multi-Layer Neural Network를 사용하여 XOR_Data를 풀어보자
.
로컬 노트북 (실습3 검색)
cf)
여태껏 Single-Layer Neural Network에서는 h(x)가 0~1사이로 나오도록 squarshing해주기 위해 한번만 sigmoid해주었으나,
Multi-Layer neural network에서는 마지막 Single-Layer이외에 앞부분에서도 계속 층마다 z(x) -> sigmoid -> a(x)를 만들어준 이유는?
각 층마다 나오는 output인 a1(x), a2(x), ... 등을 output function을 위한 sigmoid이다.
output function은 덧셈*곱셈밖에 안하는 단순한 딥러닝의 계싼복잡도를 높혀주는 기능정도로 생각하자.
마지막 층인 single-layer에서 사용된 마지막 sigmoid는 0 ~1사이 값으로 변환시켜주는 activation function 중 하나인
squarsh function을 위한 sigmoid이다.
실습 - MNIST(multi-classification) 문제를 Multi-Layer Neural Network로 풀어보자.
MNIST(multi-class classification)을 Multi-Layer N.N.로 풀어보기(로컬)
3회차에서 푼 MNIST by Single-Layer의 정확도는 80%까지 올라갔었다.
이 MNIST문제(multi-classification) 를 Multi-Layer( 1개의 hidden-Layer 추가 및 노드는 1000개 )로 구성하여 풀어보고, 정확도를 비교해보자.
과정)
1. 모듈 import 및 keras.dataset에서 mnist 데이터 가져오기 -> 가져온 데이터의 shape찍어서 확인하기
2. 가져온 데이터의 label( y_train)값을 찍어본 뒤, -> figure,axes에 X_train집어넣었을 때, matshow로 그려지나 확인하기
3. Convolutional N.N.이 아닌 이상, feautre인 픽셀을 가로x세로 -> 하나로 통합하기 위한 reshape해주기
- X_train/X_test ( 데이터수, 가로pixel, 세로pixel ) ---- reshape ---> ( 데이터수, pixel수 = feature수 )
4. y_train(label) / y_test 을 원핫인코딩 해주기
- 그래야 y_predict도 원핫인코딩 형태로 예측값이 나옴.
5. classification 문제이므로
1) z(x)에 입힐 sigmoid함수 정의
2) loss 확인용 cross-entropy함수 정의 -> hot버전의 (actual = y_train_hot, predict = y_predict_hot)이 들어간다.
6. Single-Layer에서 사용하던 Multi-classification버전의 그라디언트 태우는 코드를 가져와서 수정하기
- 임의로 뉴런( = 노드)를 가운데 1000개를 준다고 생각하자.
- w,b 1묶음이 w1, w2, b1, b2 2개의 묶음으로 늘어난다.
- forward propagation부분이 늘어난다. 아직 ont-hot-encoding버전이다.
- bacward propagation부분이 생긴다. 아직 ont-hot-encoding버전이다.
- 정확도 비교는 argmax(axis =1)으로 다시 원래 label형태로 롤백하고 난 뒤 비교한다.( binary문제면, y_predict를 0.5기준으로 squarshing후 비교)
- loss가 올라가는 발산의 상황에서는, 지금수준에서는 learning_rate를 1/10씩
- loss가 왔다갔다하는 오실레이트 상태에서도 learing_rate를 1/10씩 줄여준다. 변화가 보이면 마지막자리수만 올려준다.
- learning_rate가 너무 적으면 weight, bias도 변화가 없어진다.
7. Train의 Result를 작성하자
- 그라디언트 코드안의 forward propagation 부분(hot버전의 h(x), y_predict_hot ) + armax로 롤백하는 부분(y_predict)까지를 복사해온 뒤 실제값인 y_train과 y_predict로 DataFrame을 만들고, 2칼럼을 비교하여 전체 accuracy를 작성하자.
- 전체 Accuracy + 만든 df.shape 및 head()를 출력해주자.
8. Test set에 대한 Result는 금방 구할 수 있다.
- 마찬가지로 h(x) + 롤백하는 부분을 복사해온 뒤, train->test로 변수를 모두 변경하자.
- 전체 Accuracy + 만든 df.shape 및 head()를 출력해주자.
Multi-Layer를 쓰는 순간부터, 계산이 너무 느려진다. --> GPU를 사용하자.
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
3. Single-Layer Neural Network For Multi-class classification문제 - 원핫인코딩 / argmax / MNIST의 등장
Binary Classification문제란 y값이 0or1(False or True를 (기준조건문).astype('int')로 squarshing)로 나오는 문제였다.
이번에는 Mulit-class Classification문제로서, 가장 기초적인 예가 categorical한 상품 분류(의류 / 가전제품/ 의약품)에 대한 것이다.
먼저 그림으로 살펴보자.
위 그림과 같이,
Binary classification문제( 0 or 1) 해결을 위해 만든 Single-Layer Neural Network를 똑같이 유지한 상태(input이 x1,x2,,xn,1로 1개)에서
카테고리 수만큼 h(x), L(y,h(x)), J(w,b) = Output를 만든 뒤, 각각의 Output( 0or1 ) 가운데 가장 높은 값을 선택하면 되는데,
실제 그라디언트 디센트 알고리즘을 태울 때는,
(1) y값(정답 0 or 1 or 2)을 One-hot-encoding( np.eye(3)[y] )을 통해 [1,0,0] [0,1,0] [0,0,1]형태로 y_hot 만들어놓고
(2) y_predict_hot까지를 [ 0.4, 0.9, 0.8]형태의 확률로 예측하게 만든다.
(3) w 업데이트에 있어서는 classification용 Log씌운 Loss function인 L(y,h(x))의 편미분결과(전과 같음)의 평균을 이용하는데
이 때, y_predict -y가 아닌, 아직 롤백전인 one-hot-coding 형태[ , , ]인 ( y_predict_hot - y_hot )을 이용한다.
만약 X.T.dot()을 썼다면, .mean()대신 / X.shape[0]을 나눠준다.
(4) accuracy를 구하기 위해서, argmax(axis=1)을 이용하여 y(정답)형태로 롤백 한 y_predict 와 y를 비교한다.
(3) 거기에 정답의형태로 롤백하기 위해,
Multi-class Classification에 있어서, 불러온 데이터로 그라디언트(SL.N.N)를 태우기 전에,
전처리해줘야할 것이 있는데 y(label)을 --> identity matrix를 이용한 One-hot encoding 과정이 필요하다.
또한, one-hot-encoding된 y값을 예측한 y_predict_hot은 .argmax(axis=1)을 통해 정답형태로 롤백해줘야 accuracy를 구할 수 있다.
실습
임시요약
Multi-class classification
1) 데이터를 퍼올 땐 feature들의 데이터를 대문자 X, label 데이터를 소문자 y를 이용해 받아온다.
2) y값은 np.eye()를 통한 one-hot-encoding으로 변형시켜주어야한다. ---> y_hot
- y는 0,1,2 순으로 정답이 나와있어야 한다.
- y의 unique한 len을 알고 있어야하며, 그것을 np.eye( )[y]인자로 넣어주어야한다.
3) y_predict_hot은 [ one-hot-encoding 된 y]의 형태로 학습된 y_hot에 대해서, w와 b를 예측하므로,
y_hot 의 1개 데이터가 = [ 0, 1, 0] 이었다면 -----> y_predict_hot = [ 0.3, 0.9, 0.5 ]형태로 나온다.
4) y_predict_hot은 argmax(axis=1)을 이용하여, y형태로 롤백된다. ---> y_predict
- argmax(aixs=1)은 3개 중 가장 높은 확률의 index를 산출해주는데, 그게 자동으로 가장 근접한 y(label)형태로 반환된다.
5) 반환된 y_predict와 y를 이용해서 조건문을 이용하여 비교하면, 150개 에 대해서 0 or 1로 나올 것이다. 그것의 평균을 정확도로 한다.
6) cost function의 편미분값으로 w를 업데이트 시켜주는 Graident 를 태울 때는, 아직 one-hot-encoding형태를 사용하여 차이를 구하는데
y_predict_hot - y_hot 으로 차이를 구한다.
- w의 경우, dot product를 이용했다면 --> .mean()대신 X.shape[0]을 통해 데이터의 개수로 나누어서 평균을 적용시킨다
- b의 경우, mean(axis=0)을 통해 150개 데이터에 대한 세로줄의 평균을 구해서 업데이트 한다.
7) y_predict 식의 검증이 끝났다면, 기존 데이터에 새로운 칼럼으로 추가해준다.
my) y는 np.eye( 라벨의 갯수) 로 원핫인코딩 ---> y_predict는 y_predict_hot에다가 argmax(axis=1)로 롤백
실습 - MNIST
어떤 문제를 Single-Layer Neural Network로 풀기로 마음 먹었다면,
X(feature)와 y(label) 데이터를 가져온 뒤,
그림을 그려봐야한다.!!!
-> MNIST( multi-classification)을 Single-Layer N.N. 버전으로 풀기 복습 완료(로컬 노트북)
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
2. Single-Layer Neural Network For Binary classification문제 - sigmoid의 등장 & squarshing
저번시간에 언급한 Single-Layer Neura Network에 대한 기본 알고리즘인 Gradient Descent를 공부했다.
전체적으로 Single-Layer Neura Network와 Perceptron과 같은 개념으로 보고, 아래와 같이 그림으로 나타낼 수 있다.
게다가 고전 알고리즘인 Linear Regression도 비슷한 개념으로 생각하자.
이러한 SLNN는 사실 Regression문제을 위한 Single-Layer Neural Network다.
그러면 Regression문제 이외에 다른 문제가 있을 까?
Regression문제 과 classification문제
기본적으로, 주어진 Data를 보고 Regression문제인지 Classification문제인지를 먼저 정의해야한다.
위 표를 참고하여, 우리가 받은 Data의 label이 높고 낮음이 중요-> Regression문제
위 표를 참고하여, 우리가 받은 Data의 label이 같냐 다르냐가 중요-> Classification문제
전통적인 알고리즘인 리니어, 로지스틱 회귀와 관련해서는
Regression알고리즘을 ---> Regression문제에 적용하여 푼 것 : Linear Regression
Regression알고리즘을 ---> Classification문제에 적용하여 푼 것 : Rogistic Regression
Binary Classification문제
Binary Classification문제는 y값의 범위가 0 or 1이다.
그러나 저번시간에 배운 Regression알고리즘(SLNN-gradient descent)의 h(x)(y_predict)값이
-무한대 ~ +무한대까지 나오므로 binary classification문제에 적용을 할 수 없다.
그러므로, 저번시간의 Regression알고리즘인 SLNN-gradient descent을 ---(???)-----> classification알고리즘으로 바꿔주어야한다.
- Regression알고리즘에서는 h(x)의 값으로 -무한대 ~ +무한대까지 나왔다.
이제 중간에, 이 값(-무한대~+무한대)를 받아서 ---> 예측값(h(x), y_predict)값이 0 or 1이 나오도록 으깨주는 새로운 함수 f(x)를 집어넣는다.
이러한 f(x)를 squarsh function이라고 하며, y값(h(x), y_predict)가 0or1으로 정의되므로
binary classification문제를 풀 수 있는 classification알고리즘이 된다. - 이 Squarsh function로 0 or 1이 나오도록 으깨어서 Regression - SLNN알고리즘에 적용시 ----> classification알고리즘이 된다.
하지만, 이 Squarsh function은 반드시 미분가능해야한다. ->
그래야 f(x)로부터 정의되는 h(x), L(y,h(x)), J(w,b) 편미분하여 -> w를 업데이트 해 줄 수 있다.
그러므로 Squarsh function의 전제조건은 - 이 전제조건(미분가능하고 0or1이 나오는)을 만족하는 Squarsh function이 바로 f(x) = Sigmoid이다.
def sigmoid(x):
return 1 / ( 1 + np.exp(-x) )
식은 아래와 같고, https://www.desmos.com/calculator 에서 그려면 그래프는 아래와 같다.
x가 무엇이 들어오든 0과 1사이로 Squarsh한다.
soomth하므로, 미분이 가능하니 --> h(x), L(y, h(x)), J(w,b)모두 미분가능하다.
여기까지 요약해보면,
저번시간에는
Regression문제(h(x), y예측값이 -무한대+무한대)를 푸는 Single-Layer Neural Network가
저번시간에 학습한 Gradient Descent이다.
이번에는
Classification문제(h(x), y예측값이 0or1) 를 푸는 Single-Layer Neural Network를 짜기위해서
Gradient Descent 알고리즘 중 h(x)값이 0or1이 나오도록 미분가능한 sigmoid를 h(x)전에 f(x)로 씌워준 시킨 뒤, 합성해주었다. h( f(x) )
하지만 여기까지만 하면 문제가 발생한다.
- sigmoid를 입힌 Loss function은 그래프상으로 울퉁불퉁해져서, 접선의 기울기가 0이지만 happy하지 않는 또다른 지점(Local obtimer)이 생겨, 정답(y_predict - y = 0)이 아님에도 불구하고 w를 업데이트 안시켜주는 현상이 생길 수 있다.
이렇게 울퉁불퉁한 h(x)를 graident로 태우면, L(y,h(x))는 느리거나 수렴하지 않을 수 있다. - sigmoid에 있는 e^x 때문에 결국에는 울퉁불퉁해진다. 이 울퉁불퉁한 것을 없애서 happ한 Loss function을 만들어주기 위해
sigmoid에 Log를 입혀 e^x를 없애 울퉁불퉁함을 없애준다.
그렇다면, sigmoid가 들어감에도 불구하고 Loss가 soomth해지기 위해 Log가 들어가야하므로
Log가 들어가는 새로운 Log function을 정의해보자.
즉, Binary Classification문제(0or1)을 풀기위한 Single-Layer Neural Network 알고리즘으로서
기존의 Graident Descent에서 sigmoid를 입힌 h(x)를 정의하고, 울퉁불퉁한 부분을 위해 Log를 입힌 Loss function
그게 Cross-Entropy 이다. - Cross-entropy의 경우에도, 역시 Loss function은 0일 때, happy / 무한대일때, unhappy하다.
증명은 아래 그림을 참고하자.
여기까지 요약하자면,
classification문제에서도 사용할 수 있는 Gradient Descent(SLNN)알고리즘을 만들기위해
1. y값이 0or1이 나오도록 squarsh function인 sigmoid를 입히고
2. 울퉁불퉁하여 미분이 되지않는 것을 방지하기 위해 Log를 입힌 Loss function이 cross-entropy이다.
이렇게 만든 Loss function은 Graident를 태울 수 있다.
우리가 실제로 쓰는 함수는 Loss function이 아니라 cost function이다.
cross-entropy(모든loss function)에서 0 or 무한대가 나오는 것을 증명을 통해 확인할 수 있는데,
만약 우리의 데이터 중에 하나라도 unhappy한 데이터로 인해 무한대가 나온다면,
전체 데이터에 대한 loss function인 cost function이 무한대가 나올 것이다.
그렇게 된다면 너무 불합리한 알고리즘이 될 수 있다.
실제 코드에서 cross-entropy를 사용할 때는,
예측값y_predict에서는 0 or 1이 나오는 것이 아니라 확률로 나온다.
그리고 그 확률을 0.5이하시 -> 0으로, 0.5 초과시 -> 1으로 분류해버릴 것이다. 이러한 것을 클리핑or쓰레숄더라고 하는데,
이렇게 한다면, Loss function에서는 y가 0or1만 가지게 될 것이므로, 무한대의 문제가 안생긴다.
- 실제로 Graident Descent를 돌리기 위한 w를 업데이트 하기 위해서는 cost function 편미분( 결국에는 loss function편미분)을 한 것이 필요하다.
- 그 과정에서는 Loss function의 편미분을 구한다.
- 그 과정에서는 h(x) = sigmoid( z(x) )의 미분이 들어간다 * sigmoid 미분 = sigmoid( 1 - sigmoid )
- Binary Classification문제를 풀기위해만든 SLNN의 알고리즘의 loss function인 Cross-entropy의 편미분 결과는
Regression문제를 풀기위한 SLNN의 알고리즘(Gradient Descent)의 loss function의 편미분 결과와 동일하고 코드도 같다.
실습
'머신러닝 & 딥러닝 > 딥러닝 - Image classification' 카테고리의 다른 글
1. Single-Layer Neural Network For Regression문제
이론
머신러닝이란?
- 우리가 쓰기위해 만든 보편적인 알고리즘
- 한국어로는 기계학습이라한다. 영어에 익숙해야져야한다. 그래야 자료를 많이 볼 수 있따.
- 머신러닝은 크게 3가지로 갈린다.
- Supervised learning(지도학습)
- label(암인지 아닌지)를 맞추는데 도움을 주는 것을 feature(성별, 나이, 혹은 픽셀)라 한다.
- x(feature) 과 y(label)이 있다. 즉, 맞추어야하는 정답에 해당하는 y값(label)이 있으면 supervised learning으로 풀어야한다.
맞추어야하는 정답에 해당하는 y값(label)이 없다면 unsupervised learning으로 풀어야한다.
- 현장(일상생활)에서는, unsupervised learning이 많이 쓰일 것이다.
왜냐하면, supervised learning은 하나의 feature당 하나의 label이 딱딱 있어야한다.
하지만, cctv/블랙박스의 많은 사진들 중 각각의 사진마다 하나의 사람을 태깅할 수 없기 때문이다. 즉, x와 y가 정확히 태깅되어있는 데이터를 쉽게얻을 수 없기 때문이다. 반면에 unsupervised learning은 각각의 feature에 해당하는 label이 있어야하는 것이 아니기 때문에, 상대적으로 알고리즘을 적용하기 쉽다.
- 그러나 실제(현장)로는 supervised learning이 많이 쓰인다. 연구하기도 쉽고 성과가 잘나오기 때문이다.
즉, 일상생활에서는 unsupervised learning이 많아야하지만, 연구와 실제(현장)는 supervised learning가 많이 쓰이고 있다|
하지만 요즘 연구의 추세는 unsupervised learning에 대한 연구를 많이 시도하고 있다.
- 간단히 말하자면, y값이 있으면 supervised / 없으면 unsupervised다.
연구를 위해서 말해보자면, y값(supervised)이 있어서 잘했는지 못했는지 가이드를 해주는 컨셉이 supervised이고,
y값이 없는데도 스스로 가이드해서 학습이 가능한 것은 unsupervised다. 1. Supervised learning(지도학습)의 분류
- Tree 모델(Decision Tree)
- Regression 모델 : 이게 딥러닝의 main
- Linear Regression
- Logistic Regression
- support vector motion
- Artficial Neural Network(ANN, 인공 신경 망)
- CNN
- RNN
2. Unsupervised learning(비지도학습)
- x(feature)만 있고 y(label)는 없다.
- x와 y가 정확하게 맞추어져있는 태깅되어있는 반드시 없어도 되므로 적용하기 쉬우나.. 연구에 있어서는 supervised가 많음
y가 많으므로. 그러나 지금은 un~으로 가는 중 왜냐하면
- 가이드가 지도해줄 y값이 없는데도 불구하고 스스로 아이가 학습하는 것. 아이가 중력/가속도를 스스로 알아낸다.3. Reinforcement learning(강화학습) :
- 알파고가 아니면 다룰 일이 없다. 앞으로 응용할 때도 없음. 응용할 곳이 별로 없다.
딥러닝?
- 마케팅적인 요소가 적혀있다. 그래서 연구쪽에서는 인공신경망이라고 말한다.
- - 딥러닝이란? 머신러닝 알고리즘(3) 중 Supervised learning 중 Regression모델 을 먼저 알아보자.
1) Linear Regression 모델- y값이 -무한대 ~ +무한대의 범위를 가지는 Regression문제를 푸는 알고리즘,
2) Logistic Regression 모델 - y값이 0 or 1이 나오는 Classification문제를 푸는 알고리즘,
- 1)과 2)는 전통적인 Regression모델이다. 이제 3)부터는 요즘시대에 말하는 딥러닝 알고리즘을 담고 있는 Regression모델
3) Atficial Neural Network(A. N. N) - 사람 뇌의 Neural Network를 모방한 컴퓨터의 알고리즘 모델
- A.N.N.은 가장 처음 나온 Single-Layer N.N. -> Multi-Layer N.N. -> Convolutional N.N. -> ... 로 발전하였다.
- A.N.N. 을 사용하여 Regression 문제와 Classification 문제를 푸는 것이 목표이며
A.N.N. 중 hidden-Layer가 3개이상 들어간 Multi-Layer N.N. 로 Regression/Classification문제를 푸는 것을 딥러닝이라 한다.
1) y값이 -무한대 ~ +무한대의 범위를 가지는 Regression문제
2) y값이 0 or 1이 나오는 Classification문제 - - 이번시간에는 하나인 Artificial Neural network 중 가장 간단한 Single-Layer Neural Network를 먼저 공부해보자.
Artficial Neural Network
이번시간엔 A. N. N. 중 가장 간단한 Single-Layer Neural Network를 배울 것이다.
- 딥러닝, 알고리즘의 특성을 나타낼 수 있는 가상의 가장 심플한 dataset을 만드는 것이 중요하다.
ANN의 dataset은 Supervised Learning으로서 기본적으로 feature와 label이 기본적으로 필요하다
- ANN은 Supervised Learning으로서 feature와 label이 있다고 했다.
- 실습은 1) Single Layer Neural Network에 관련된 RandomSearch / h-step Search / Gradient Descent 모델을 학습할 것이다.
실습 - 생략
이론2 - Gradient Descent 자세히 알아보기
머신러닝 3가지 중에 Supervised Learning은 x들과 더불어 y(답)이 있는 학습방법이다.
그 중 Regression 모델인 ANN, RNN, CNN, 선형회귀, 로지스틱회귀 등이 있지만, 그 중 ANN을 다루고 있다.
- Artficial Neural Network
- Single-Layer Neural Network
- Multi-Layer Neural Network
- Convolutional Nerual Network
Single-Layer Neural Network와 perceptron은 동일한 개념이라고 생각하자.
- y(답)과 x(feature들) 있는 어떠한 데이터가 주어졌다고 가정하자. (x는 여러개 일 수 있지만 하나라고 가정)
이러한 데이터는 Supervised learning을 적용할 수 있고, 그 중에 Regression 모델을 쓴다고 했을 때,
A.N.N 중 가장 간단한 S.L.N.N.로 Regression문제를 풀 때는, feature에서 -> label예측값을 도출해내는 weight와 bias를 구해야한다.
이러한 과정을 Optimalization이라고 한다.
이러한 최적화 기법에는 여러가지 방식(Random Search, h-step Search, Gradient Descent)이 있지만,
그 가운데 가장 효율적으로, A.N.N.을 학습시켜 weight와 bias를 구하는 알고리즘이 Gradient Descent이다..
- 기본적으로 앞으로 학습하는 모든 A.N.N.은 이 Gradient Descent를 사용해서 학습시킬 것이다.
- Gradient의 핵심은 loss, cost function을 편미분하여 w와 b의 업데이트량을 구할 수 있는 알고리즘이다.
- 제대로 학습되었다면 좋은w(배점, weight)와 b(bias)를 찾아내서 -> 다음data에 대한 y를 예측할 수 있다. 이러한 S.L.N.N.로서 문제를 풀 때, w와 b를 잘 찾아냈는지를 나타내는 함수가 Loss function이다. - 즉, 답을 알고 있는 data를 보고서, w와b를 예측하여, 다음의 답을 예측할 때
Single-Layer Neural Network를 사용해서 풀고자 한다면, - 가장 먼저해야할 것은 Hypothesis function -> Loss function -> Cost function을 정의하는 것이다.
- 다음은 Cost function을 w에 대해 편미분하여 -> 더 나은 w(점프거리)를 대략적으로 알아서 업데이트 시켜주는 것이다.
- 결과적으로는 Loss function만 편미분 해주면, 알아서 나온다. - 마지막으로 epoch-loop 수와 learning_rate를 통해 좀더 정확하게 w를 업데이트 해준다.
- Loss function(y, h(x)) -( w에 대한 2차함수) 을 편미분하여
Gradient Descent 알고리즘 속에서 갱신해줘야할 w의 방향성과 양을 대략적으로 알 수 있다고 했는데
그림으로 표현해보면 아래와 같다.
- L(y,h(x))를 편미분한 것이 w의 점프거리 갱신량과 대략적으로 비슷하다
- 그래프상 접선의 기울기가 0이라면, 갱신할 것도 없이 w와 거의 같다. 기울기가 가파르다면 갱신량이 많은 안좋은 경우다..
- 정확한 w의 갱신량은 epoch을 통한 loop와 learning_rate가 결정해 줄 것이다.
Loss function에 대해 정리하자면
Regression문제를 - S.L.N.N.로 이용해서 풀 때,
정의한 Loss function( L(y,h(x) = 1/2 ( h(x)-y)^2 )는 0이면 error가 0이라서 좋고, 무한대로 나오면 error가 큰 안좋은 경우다
그러므로 w를 계속 업데이트 시켜서 h(x)-y = 0이 나오도록 만들어야 하는데,
Loss function의 편미분한 값은 w를 찾아가는 점프거리를 반복해서 갱신해주는 방향성과 양(w변화량)을 의미한다.
그래프상으로 접선의 기울기이다.
참고) Regression문제에 쓰이는 Loss function을 MSE(mean square error) = 1/2 ( y_predict - y)^2 이라 한다.
앞으로나올 classification문제에 쓰이는 Loss functiond을 Cross-entropy라 = -y*log(h(x)) - (1-y)log(1-h(x)) 한다. - Cost function은 결국에는 Loss function을 미분하면 되지만, 증명해보자.
- 결과적으로 코드상의 매칭은
h(x) = wx+b ---> y_predict
L(y,h(x))의 편미분 ---> w 의 변화량(점프거리 갱신)의 대략적인 것
J(w,b)의 편미분 ---> w의 변화량(learning_rate = 람다 제외)
그리고 y_predict(예측값)에 해당하는 함수가 hypothesis function이다
Loss function이 하나의 데이터에 관한 얘기라면, Cost function은 전체 데이터에 관한 Loss function이다
실제 데이터를 S.L.N.N.로 분석해보기
어떠한 데이터를 보고서, label 칼럼에 대한 label(predict) 칼럼을 생성할 것이다.
예를 들어, 보스턴 집값에 대한 데이터를 가지고, 집값을 예측하는 알고리즘을 Gradien Desecent(Single-Layer Neural Network)로 만들어서 예측하자.
- numpy와 pandas 패키지를 import한다.
- Dataset을 데이터프레임으로 만든다.
- 데이터 중에 칼럼명만 나열된 칼럼이 있다면, 가져와서 columns인자로 같이 DataFrame으로 만든다.
- 데이터 중 target인 label데이터가 따로 있다면, label만 받아와서 DataFrame의 칼럼으로 추가해준다.
- 만든 데이터는 shape와 head()를 확인한다. - Gradient Descent 기본 코드를 가져와 적용해보자.
- 데이터의 각 feature에 해당하는 칼럼들을 x1, x2로 받자. 각 데이터 수만큼 리스트로 들어갈 것이다.
- for문에 들어가기 전에,
num_epoch과 learning_rate는 기본적으로 시작
w는 feature수만큼 랜덤균등분포로 -1.0 ~ 1.0으로 생성
b는 1개만 랜덤균등분포로 -1.0 ~ 1.0으로 하나 생성
- for문 안에서는 돌면서 더 해피한 값으로 갱신들어야 할 것인
y_predict 계산식이 있다. feature수만큼 수정해준다.
error(예측값- 정답에 절대값씌운 평균)식은 그대로다.
if error < 기준error값: break의 기준error값도 수정해준다.
*기준error값은 해당 데이터의 y(label)을 기준으로 생각해준다.
*만약, 집값 예측이라면, error기준이 5로 주어도, 5000달러(500만원)으로서 에러범위로서는 충분하다.
if epoch 갯수별 print는 0 : 해당epoch과 1: error 수치만 띄워주도록한다.
w값과 b 갱신식을 만들어준다. feature수에 맞게만 만들어주면 된다. - 만일 epoch 100, learning_rate 100으로 시작했는데, error가 줄지않고 늘면서 발산한다면,
- 가장 만만한 것은 learning_rate를 줄여주는 것이다.
*너무 줄이면, w가 없데이트가 안됨->y예측값 그대로->error도 그대로-> 발산 그대로-> 올려줘야함. 다른 것을 수정하더라도 error가 멈쳐있으면 learning_rate를 올려줘야함.
- 1.0 -> 0.1 -> 0.01 -> ...-> 0.00001 식으로 나누기10씩 소수점을 넣어준다.
- 0을 늘려줬는데, 발산하면 다시 0을 줄인다.
- 그다음 마지막 자리수를 1->2->3으로 늘여준다.
- 그다음 epoch을 10000, 100000 씩으로 늘여준다.
- epoch만큼 print 단위와, 자리수배열을 예쁘게 만들어준다.
* 딥러닝은 data에 따라 configuration(hyper-parameter)이 천차만별로 바뀌기때문에 tensorflow코드만 가져온다고해서 실행이 되지않는다. 그러므로 이론을 자세히 공부한 상태에서 응용이 가능하다. - 이제 원하는 기준error수준으로 label이 예측가능해지면, 결과값을 뽑아낸다.
- y_predict식을 가져와서 예측값을 데이터수만큼 확인해본다.
- dataFrame을 .copy()해서 result라는 새로운df에 옮겨담는다.
- y_predict를 데이터의 label예측 칼럼(predict)으로 추가해준다.
Single-Layer Neural Network도 실전에 이용할 수 있다.
real데이터에서도 어느정도 성능이 보장된다.
dot product
지금은 13개의 feature밖에 안되지만, 만약 feature가 300개가 넘어가면 y_predict 식을 작성하기가 쉽지가 않다. 그 때 쓰는 것이 dot product이다.
위의 그림를 보면, y_predict 계산식에서 가로는 x, 세로는 w가 될 것이다.
- feature의 수만큼 생성했던 w를, 한번에 생성해도 된다.(size=13인자)
- X에서는 feature들만 모아놓았기 때문에, y_predict = X(506 ,13).dot(w(13,1))+b 로 한번에 계산된다.
- w를 업데이트해줄 때, 기존은 w = w - learning_rate * ( (y_predict - y)*x).mean()
- feature 데이터만 모아놓은 X에 dot()을 적용하여, 순서대로 앞의 y_predict-y와 곱해져야한다.
- X(506, 13)를 X.T로서 (13, 506)로 바꾸고,
- y_predict - y(506, 1)을 dot하여 (13, 506)dot(506,1) -> (13,1)의 w데이터가 각각 업데이트 될 것이다.
- 이제 .mean()의 개념을 도입하기 위해서, for문전에 num_data = X.shape[0]을 통해 X의 (506, 13)중 데이터의 수를 의미하는 506을 가져와서 나눠준다. - 만약, 공식상에서 나온 행렬의 곱에 dot product를 적용시킬 때, shape가 맞지 않아서 계산이 안된다면,
1) 뒤에놈을 .T로 변형시키고
2) 그놈을 앞으로 빼서 .T.dot( ) 해주면 된다.
예를 들어, X(506데이터, 13feature수) * w(feature수13, output수 1)는 바로 X.dot(w)로 적용이 되지만
w의 업데이트량을 의미하는 y_predict - y ( 506, 1 ) * X(506, 13) 의 계산에서는
1) X.T(13, 506) -- y_predict-y(506, 1) 로 뒤에것을 T.로 뒤집고
2) X.T.dot( y_predict -y ) 로 앞으로 빼서 dot을 적용시킨다.


























































































































































































































































